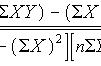这个公式计算每次迭代时θ的变化量。
α(α)被称为学习率,学习率决定了每次迭代的步骤有多大。好的学习率是非常重要的,因为如果它太大,算法不会达到最小值,如果它太小,算法会花很长时间才能达到。在本例中,我们设置alpha为0.001。
步骤如下:
估计θ;
计算成本;
调整θ;
重复2和3,直到达到最佳效果。
这是我使用梯度下降实现简单线性回归的方法。
斜率和截距都是0,0。
注:在机器学习中,我们使用θ来表示向量[y-截距,斜率]。θ=y轴截距。θ1=斜率。这就是为什么在下面的实现中将theta看作变量名。
# x = [58, 62, 60, 64, 67, 70] # 妈妈的身高
# y = [60, 60, 58, 60, 70, 72] # 女儿的身高
class LinearRegression:
def __init__(self, x_set, y_set):
self.x_set = x_set
self.y_set = y_set
self.alpha = 0.0001 # alpha 是学习率
def get_theta(self, theta):
intercept, slope = theta
intercept_gradient = 0
slope_gradient = 0
m = len(self.y_set)
for i in range(0, len(self.y_set)):
x_val = self.x_set[i]
y_val = self.y_set[i]
y_predicted = self.get_prediction(slope, intercept, x_val)
intercept_gradient = (y_predicted - y_val)
slope_gradient = (y_predicted - y_val) * x_val
new_intercept = intercept - self.alpha * intercept_gradient
new_slope = slope - self.alpha * (1/m) * slope_gradient
return [new_intercept, new_slope]
def get_prediction(self, slope, intercept, x_val):
return slope * x_val intercept
def calc_cost(self, theta):
intercept, slope = theta
sum = 0
for i in range(0, len(self.y_set)):
x_val = self.x_set[i]
y_val = self.y_set[i]
y_predicted = self.get_prediction(slope, intercept, x_val)
diff_sq = (y_predicted - y_val) ** 2
sum = diff_sq
cost = sum / (2*len(self.y_set))
return cost
def iterate(self):
num_iteration = 0
current_cost = None
current_theta = [0, 0] # 初始化为0
while num_iteration < 500:
if num_iteration % 10 == 0:
print('current iteration: ', num_iteration)
print('current cost: ', current_cost)
print('current theta: ', current_theta)
new_cost = self.calc_cost(current_theta)
current_cost = new_cost
new_theta = self.get_theta(current_theta)
current_theta = new_theta
num_iteration = 1
print(f'After {num_iteration}, total cost is {current_cost}. Theta is {current_theta}')
使用这个算法和上面的母女身高数据集,经过500次迭代后得到了3.4的成本。
500次迭代后的方程为y=0.998x 0.078,实际回归线为y=1.2x-12.87,成本约为3.1。
用[0,0]作为[y-截距,斜率]的初始值,得到y=1.2x-12.87是不切实际的。为了在没有大量迭代的情况下接近这个目标,必须从一个更好的初始值开始。
例如,[-10,1]在不到10次迭代后,大约得到y=1.153x-10,成本为3.1。
在机器学习领域,调整学习率和初始估计等参数是比较常见的做法。
这就是线性回归中梯度下降的要点。
梯度下降法是一种通过多次迭代最小化误差平方和来逼近最小平方回归线的算法。
到目前为止,我们已经讨论过简单线性回归,其中只有1个自变量(即一组x值),但理论上梯度下降可以处理n个变量。
下面重构了之前的算法来处理n个变量。
import numpy as np
class LinearRegression:
def __init__(self, dataset):
self.dataset = dataset
self.alpha = 0.0001 # alpha 是学习率
def get_theta(self, theta):
num_params = len(self.dataset[0])
new_gradients = [0] * num_params
m = len(self.dataset)
for i in range(0, len(self.dataset)):
predicted = self.get_prediction(theta, self.dataset[i])
actual = self.dataset[i][-1]
for j in range(0, num_params):
x_j = 1 if j == 0 else self.dataset[i][j - 1]
new_gradients[j] = (predicted - actual) * x_j
new_theta = [0] * num_params
for j in range(0, num_params):
new_theta[j] = theta[j] - self.alpha * (1/m) * new_gradients[j]
return new_theta
def get_prediction(self, theta, data_point):
# 使用点乘
# y = mx b 可以重写为 [b m] dot [1 x]
# [b m] 是参数
# 代入x的值
values = [0]*len(data_point)
for i in range(0, len(values)):
values[i] = 1 if i == 0 else data_point[i-1]
prediction = np.dot(theta, values)
return prediction
def calc_cost(self, theta):
sum = 0
for i in range(0, len(self.dataset)):
predicted = self.get_prediction(theta, self.dataset[i])
actual = self.dataset[i][-1]
diff_sq = (predicted - actual) ** 2
sum = diff_sq
cost = sum / (2*len(self.dataset))
return cost
def iterate(self):
num_iteration = 0
current_cost = None
current_theta = [0] * len(self.dataset[0]) # initialize to 0
while num_iteration < 500:
if num_iteration % 10 == 0:
print('current iteration: ', num_iteration)
print('current cost: ', current_cost)
print('current theta: ', current_theta)
new_cost = self.calc_cost(current_theta)
current_cost = new_cost
new_theta = self.get_theta(current_theta)
current_theta = new_theta
num_iteration = 1
print(f'After {num_iteration}, total cost is {current_cost}. Theta is {current_theta}')
唯一调整的是不用mx b(即斜率乘以变量x加y截距)来获得预测值,而是进行矩阵乘法(参见上述的def get_prediction)。

使用点积,你的算法可以接受n个变量来计算预测。
,