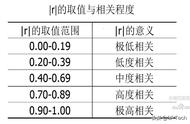
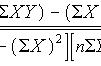误差是实际值减去预测值,最佳拟合线使所有误差平方和最小化。在线性回归中,我们用相关系数计算出的最佳拟合线也恰好是最小平方误差线。这就是回归线被称为最小二乘回归线的原因。
最佳拟合线是最小二乘回归线。
在下面的图像中,直线C比直线B更适合,直线B比直线A更适合。

这就是梯度下降的工作原理:
从一条随机线开始,比如说直线a,我们计算这条线的误差平方和,然后调整斜率和y轴截距,重新计算新行的误差平方和。继续调整,直到达到局部最小值,其中平方误差之和最小。
梯度下降法是一种通过多次迭代最小化误差平方和来逼近最小平方回归线的算法。
梯度下降算法
在机器学习术语中,误差平方和称为“成本”(cost)。这个成本公式是:


因此,这个方程是“误差平方和”,它计算的是预测值减去实际值平方的总和。
1/2m是“平均”数据点数量的平方误差,这样数据点的数量不会影响函数。(除以2的原因请见此链接:
在梯度下降中,目标是使代价函数最小化。我们通过尝试不同的斜率和截距值来实现这一点。但应该尝试哪些值?又如何改变这些值呢?
我们根据梯度下降公式改变它们的值,这个公式来自于对代价函数的偏导数。(确切的数学公式可以在这个链接中找到:
通过偏导数,得到: