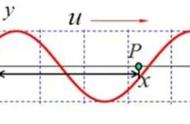
设一个质点在同一方向上同时进行两个独立的同频率的简谐振动。取这一方向直线为x轴,质点的平衡位置为坐标原点,则在任意时刻t这两个简谐振动的位移可分别表示为
x1=A1cos(ωt φ1)
x2=A2cos(ωt φ2)
由于两个简谐振动处于同一方向,直线上则任意时刻和振动的位移为x=x1 x2

虽然利用三角公式不难求得合成结果,但是利用简谐振动的矢量图示法可以更简洁直观地求出物体所参与的合振动。
两个分振动分别与旋转矢量A1与和和A2相对应,在t=0时,A1、A2与x轴的夹角分别为φ1、φ2。由于A1、A2以相同的角速度ω逆时针旋转,所以它们之间的夹角不变,因而合成矢量A的大小亦不变。
从图中可以看出,任一时刻合矢量A在x轴上的投影x正好等于该时刻A1和A2在x轴上的投影x1和x2的代数和。因此,矢量A就是和振动所对应的旋转矢量,合振动的表达式为x=Acos(ωt φ)
可见,合振动是一简谐振动,频率与分振动频率相同。利用矢量合成法对应几何关系,可以求得和振动的振幅A和初相位φ分别为

由上式可知,和振动的振幅和初相位都与两个分振动的振幅和初相位有关。对于k=0,1,2,…,得
(1)若相位差φ2-φ1=±2kπ时,
A=A1 A2,合振幅最大。
(2)若相位差φ2-φ1=±(2k 1)π时,
A=│A1-A2│,合振幅最小。
(3)当相位差取其他值时,
│A1-A2│<A<│A1│ │A2│。

例题:两个同方向,同频率的简谐振动表达式分别为。试求它的和振动表达式。