三角形线段计算公式,求三角形线段长度最简单的方法

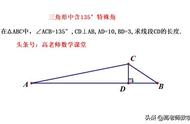
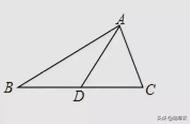
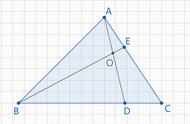
如图，在RT△ABC中，∠ABC=90°，AB=4，AD平分∠BAC，BD:CD=3:5，点E为AC的中点，ED的延长线交AB的延长线于点F，则BF=_________.

1、题目中告知了哪些主要条件？

角平分线、比例、中点，还有一个直角。

2、题目属于什么类型？通常用什么方法来求解？

求线段长，通常用勾股或相似来求解。

3、不作辅助线能不能求解？

不能。

①从勾股考虑，有现成的直角三角形△BDF，但是没有一条已知边，BF也无法与BD或DF建立联系。

②从相似考虑，现有图形中并不存在相似三角形。

综合判断，需要作辅助线。

4、怎样作辅助线？

需结合已知条件来考虑。

由中点可以联想到构造中位线、直角三角形斜边上的中线；由比例可以联想到构造相似三角形，通常要作平行线；由角平分线可以联想到角平分线的性质，通常要作垂线。

解：取BC中点G，连接EG.

则EG//AB，EG=AB/2=2

设BD=3m，CD=5m，则BG=CG=4m

∴DG=CD-CG=5m-4m=m

∵EG//BF

∴△DGE∽△DBF

∴EG:BF=DG:BD，即2:BF=m:3m

∴BF=6

以上解法是构造8字相似来求解，本题也可构造A字相似求解。

由BF:FH=BD:EH，可得

BF:(BF 2)=3:4，同样可得BF=6.

通过上面的解法不难发现，题目中的角平分线和直角从头到尾都没有用过，属于多余条件。这两个条件的出现，一是起到一定的干扰作用，二是为本题的解法提供了更多的可能性。