如图,△ABC中,D是BC边上一点,E是AC边上一点。BD=3DC,EC=2AE。BE与AD相交于O,求△ABC被分成的四个部分面积各占△ABC的比例。

这是一到非常经典的线段比例计算题,线段比例只是个过程,目标是求面积的比例。其实基本思路就是“同高三角形的面积比例等于底边比例”和“同底三角形的面积比例等于高长比例”。江湖上很多人喜欢把这种类似的形状称为燕尾模型,但大可不必这么强硬地用某种所谓XX模型来生搬硬套。因为只要反复利用上述两个知识点就能解决问题。下面简单记录一下这两个知识的原型:
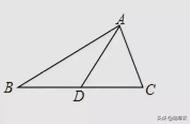
1.在△ABC中,S△ABD:S△ACD=BD:DC

即“同高三角形的面积比例等于底边比例”
2.在△ABC中,S△AOB:S△AOC=BD:DC

即同底三角形的面积比例等于高长的比例
(BD:DC其实就是高长的比例,可以做垂线,很容易计算相似的直角三角形相似比)
那么这道题目就是反复使用这个方法来求解。
首先,四边形CDOE是不规则四边形,容易想到应该将其分隔为规则形状,自然会想到连接CO,分割成两个三角形,这样才容易计算面积。

接下来就是计算面积的比值了。
因为△AOE的面积最小,所以不妨设△AOE的面积为S(或者为方便计算设为1也可以),其他图形的面积就较容易表示了。
∵S△AOE=S
∴S△AOC:S△AOE =2:1
∴S△AOC=2S
∵S△AOB:S△AOC=BD:CD=3:1
∴S△AOB=9S
∵S△BCE:S△BAE=2:1
∴S△BCE=20S
∴S△BOC= S△BCE-S△COE=18S
∵△BOC被分隔为△BOD和△COD,且S△BOD:S△COD=BD:DC=3:1
∴S△BOD=3/4 • S△BOC=3/4 •18S=13.5S
S△COD=1/4 • S△BOC=4.5S
那么,四个部分各占整个三角形的比例就容易计算了吧。
,