同一平面内的两条直线相反不相交,同一平面内不相交的两条直线叫做

三线八角图（重点、难点）

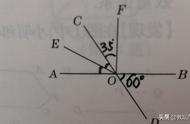
如图，判断下列各对角的位置关系：

(1)∠1 与∠2；(2)∠1 与∠7；(3)∠1 与∠BAD；(4)∠2 与∠6；(5)∠5 与∠8.

解：我们将各对角从图形中抽出来(或者说略去与有关角无关的线)，得到下列各图.

如图所示，不难看出∠1 与∠2 是同旁内角；∠1 与∠7 是同位角；∠1 与∠BAD是同旁内角；∠2 与∠6 是内错角；∠5 与∠8 对顶角.

注意：图中∠2 与∠9，它们是同位角吗？

不是，∵∠2 与∠9 的各边分别在四条不同直线上，不是两直线被第三条直线所截而成.

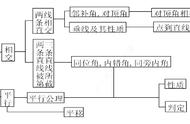
5.2 平行线及其判定

1.平行线的概念：在同一平面内，不相交的两条直线叫做平行线，直线a与直线b互相平行，记作a ∥b .

2.两条直线的位置关系在同一平面内，两条直线的位置关系只有两种：(1)相交；(2)平行.

因此当我们得知在同一平面内两直线不相交时，就可以肯定它们平行；反过来也一样(这里，我们把重合的两直线看成一条直线).

判断同一平面内两直线的位置关系时，可以根据它们的公共点的个数来确定：

①有且只有一个公共点，两直线相交；②无公共点，则两直线平行；③两个或两个以上公共点，则两直线重合(∵两点确定一条直线)

3.平行公理――平行线的存在性与惟一性经过直线外一点，有且只有一条直线与这条直线平行

4.平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行.