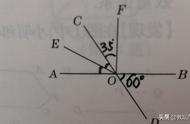
证明:∵∠1=∠B(已知)
∴DE∥BC(同位角相等,两直线平行)
∴∠2=∠C(两直线平行,同位角相等)
例2:如图,AB∥DF,DE∥BC,∠1=65°求∠2、∠3的度数.

解:∵DE∥BC∴∠2=∠1=65°(两直线平行,内错角相等)
∵AB∥DF∴∠3+∠2=180°(两直线平行,同旁内角互补)
∴∠3=180°-∠2=180°-65°=115°
例3:如图,直线AB,CD分别和直线MN相交于点E,F,EG平分∠BEN,FH平分∠DFN.若AB∥CD,你能说明EG和FH也平行吗?

错解:∵EG平分∠BEN,∴∠BEG=12∠BEN.
同理,∵FH平分∠DFN,∴∠DFH=12∠DFN.又∵AB∥CD,∴∠BEN=∠DFN;从而∠BEG=∠DFH.∴EG∥FH.
错解分析:在复杂的图形中正确地找出同位角、内错角或同旁内角,是运用平行线的判定或性质的前提.认清一对同位角、内错角或同旁内角的关键是弄清截线和被截线,截线就是它们的公共边,其余两条边就是被截线.而 ∠BEG 和∠DFH 不是直线 EG,FH 被某条直线所截得的同位角, ∴由 ∠BEG=∠DFH 不能判定EG∥FH.
正解:∵EG平分∠BEN,∴∠BEG=∠GEN=12∠BEN,
同理,∵FH平分∠DFN,∴∠DFH=∠HFN=12∠DFN,
又∵AB∥CD,∴∠BEN=∠DFN,从而∠GEN=∠HFN.
而∠GEN,∠HFN是直线EG,FH被直线MN所截得的同位角,∴EG∥FH.
例4:如图,△ABC中,已知∠1 ∠2=180°,∠3=∠B, 试判断DE与BC的位置关系,并说明理由.

错解:∵∠1 ∠2=180°,∴EF∥AB.
∴∠3 ∠BDE=180°.
∵∠3=∠B,∴∠B ∠BDE=180°.
∴DE∥BC.
错解分析:由∠1+∠2=180°,不能得到EF∥AB.虽然∠1和∠2是由直线EF和AB被直线DC所截得的角,但由于它们不是同旁内角,∴尽管∠1+∠2=180°, 也不能得到EF∥AB.
正解:∵∠1=∠4,∠1+∠2=180°,∴∠2 ∠4=180°.
∴EF∥DB(同旁内角互补,两直线平行).
∴∠3 ∠BDE=180°(两直线平行, 同旁内角互补).
∵∠3=∠B,∴∠B ∠BDE=180°.
∴DE∥BC(同旁内角互补,两直线平行).
5.3.2命题、定理、证明1.命题的概念:判断一件事情的语句,叫做命题.
2.命题的组成每个命题都是题设、结论两部分组成.题设是已知事项,结论是由已知事项推出的事项.
3.如果题设成立,那么结论一定成立,这样的命题叫真命题.如果题设成立,不能保证结论一定成立,这样的命题叫做假命题.
4.经过推理证实而得到的真命题叫做定理.
5.在很多情况下,一个命题的正确性需要经过推理才能作出判断,这个推理过程叫做证明.
5.4平移
1.平移变换
①把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
②新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点③连接各组对应点的线段平行且相等
2.平移的特征:
①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化.
②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.
例:如图,△ABC经过平移之后成为△DEF,那么: