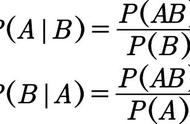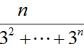两个事件一起(或依次)发生的概率。
例如:掷硬币的概率是 ¹⁄₂ = 50%,翻转 2 个公平硬币的概率是 ¹⁄₂ × ¹⁄₂ = ¹⁄₄ = 25%(这也可以理解为 50% 的 50%)
P(A ∩ B) = P(A) ⋅ P(B)
对于 2 个硬币,样本空间将是 4 {HH,HT,TH,TT},如果第一个硬币是 H,那么剩余的结果是 2 {HT,HH}。 这意味着第一个事件可能会影响第二个事件。
例如:从 10 个不同颜色的球中选出 1 个绿球的概率是 ¹⁄₁₀, 10个球中选2个绿球的概率(2个绿、2个蓝、2个红、4个黄)²⁄₁₀ × ¹⁄₉(这个排列组合会更清楚)
简而言之。 当第一个事件的发生影响第二个事件的发生时,它们是相关事件。
P(A ∩ B) = P(A) ⋅ P(B|A)
这里,P(B|A) 被读作 在 A 之后发生 B 的概率。这是当 A 事件已经发生时发生 B 事件的概率。 这称为条件概率。
联合概率和条件概率例:城市中的一个三角形区域被化学工业污染。 有2%的孩子住在这个三角区。 其中 14% 的检测过量有毒金属呈阳性,而不在三角区居住的城市儿童的阳性检测率仅为1%。
考虑: T 表示居住在三角形区域的人,并且P 表示检测呈阳性的人。
当它说区域中 14% 的孩子测试为阳性时,这意味着:如果从三角形中随机抽取一个孩子,它将有 14% 的机会测试为阳性。 这是 P(P∣T)
P(P∩T) 的解释是自整个人口中随机选择后即在三角形中并且测试为阳性的概率。
用维恩图理解P(A∩B) 是 A 和 B 都发生的概率(没有任何附加信息。)

P(A|B) 是如果我们知道 B 已经发生,A发生的概率。

让我们通过一个例子来理解它。一个班有60名学生。 33个喜欢蓝色,23个喜欢红色,20个学生喜欢这两种颜色,4个学生喜欢橙色。
1、选出一个同时喜欢红和蓝颜色的学生的概率是多少?
这非常简单:P(B ∩ R) = ²⁰⁄₆₀
2、从喜欢红色的学生中选出一个喜欢蓝色的学生的概率是多少?
我们将检查从特定学生集中选择具有特定选择的学生的概率。
⇒ 喜欢红色的学生有 23 人。其中有 20 个喜欢这两种颜色。
P(B | R) =²⁰⁄₂₃
通过维恩图和上面的例子,我们可以说在这两种情况下,事件的结果都没有改变,但样本空间正在减少。因此,
(∣) ≥(∩)
更多的例子例子1:

假设掷两个骰子,第一个得到6第二个得到4的概率是多少? 假设掷两个骰子,如果两个骰子的数字之和是10,第二个骰子显示4的概率是多少?
在第一种情况下,没有给出定义样本空间的条件。所以我们从两个骰子中取可能的结果,也就是36。
P(a∩b) = 2/36
在第二种情况下,对于样本空间有一个条件,即骰子上的两个数的样本空间总和为10。样本空间的总元素只有3 {4 6,5 5,6 4}
P(a | b) = 1/3
例子2: