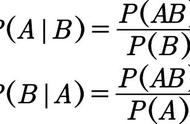一个人正在过马路,我们想计算他被路过的汽车撞到的概率,这取决于交通灯的颜色。
设H代表这个人是否被撞,C代表红绿灯的颜色。
H ={撞,不撞}
C ={红、黄、绿}。
在这种情况下,你被撞到的条件概率是概率P(H=撞到|C=红色),即假设灯是红色的,你被车撞到的概率有多大。
即使不是红灯,也有可能有人被撞到,但这里我们只考虑红灯时发生的车祸。
而联合概率则是P(H=撞到,C=红色),即红灯亮时你被车撞到的概率。

假设一个人横穿马路 3 次而没有发生事故。但第7次被撞了。 如果使用联合概率,我们还想知道当他被撞时灯是红色的概率是多少。
现在如果我们说,他在红灯时过马路10次,被车撞了7次。 在这种情况下,样本空间的条件是已经给定的。
例子3:
研究人员调查了100名学生,询问他们最想拥有哪种超能力。这个双表格显示了参与调查的学生样本的数据:

我们来找出不同的概率;
1、找出学生选择飞行作为他们超能力的概率。
没有给出样本空间的条件。我们取所有学生(100)来计算概率。
P(fly) = 38/100 = 0.38
2、求出该学生是男性的概率。
同样,没有给出样本空间的条件。我们取所有学生(100)来计算概率。
P(male)= 48/100 = 0.48
3、求选择飞行作为超能力时,这个学生是男性的概率。
这很有趣,这个问题的样本空间是一群想要飞行的学生。
n (S) = 38
38名学生中有26名是男性。所以
P(male∣fly) = 26/38 = 0.68
或者用条件概率公式
P(male∩fly) =选择飞行男生/总人数= 26/100
P(male∣fly)= P(male∩fly)/ P(fly)= 26/38 = 0.68
4、假设该学生是男性,求出该学生选择飞行的概率。
这和上一题差不多。这个问题的样本空间为n(S) = 48。在48名学生中,有26人选择飞行。所以
P(male∣fly) = 26/48 =0.68
5、I代表一个学生选择隐身作为超能力的事件,F代表一个学生是女性的事件。
解释P(I∣F)≈0.62的含义;
a、大约62%的女性选择隐身作为她们的超能力。
b、在选择隐身作为自己超能力的人中,大约有62%是女性。
解释如下:
n(S) =所有女性,I∣F可以被解读为在所有女性中选择隐身的人。
总的来说,我们可以理解为大约62%的女性选择隐身作为她们的超能力。所以表述a是正确的。
例子4:
下表是将各国按地区和平均创业成本(占某一年人均国民总收入(GNI)的百分比)进行了分类。

考虑到如果该国的创业成本归类为高,那么找出该国位于南亚地区的概率。
这个问题属于条件概率,因为给定了选择样本空间的条件:创业成本高的国家 n(S) = 87(样本空间), 以上样本空间中的南亚地区国家,即创业成本高的国家:7
所以,从创业成本高的国家中选择南亚地区国家的概率= 7/87
如果我们用条件概率的公式