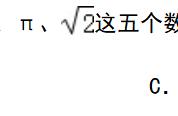大家对乘法口诀一定熟记于心,例如二二得四、三三见九,四四一十六,五五二十五,因此四的算术平方根为二,九的算术平方根为三,十六的算术平方根是四,二十五的算术平方根是五。
然而,负数的平方根是什么样呢?square(-1)和square(-5)之类的表达式有什么意义吗?
如果从有理数(实数)的角度来揣想这样的数,你一定会得出结论:这样的式子没有任何意义,你一定不是一个人在战斗,12世纪的印度数学家拜斯伽罗已经给出结论:“正数的平方是正数,负数的平方也是正数。因此一个正数的平方根是两重的:一个正数和一个负数。负数没有平方根,因为负数并不是平方数。”但是数学家的脾气倔强得很,如果有些看起来没有意义的东西不断在数学公式中冒头,他们就会尽可能创造出一些意义来。那么负数的平方根就在很多地方冒过头,既在古老而简单的算术问题上出现,也在20世纪相对论的时空结合问题上露面。那么谁是第一个“吃螃蟹”的勇士呢?是16世纪的意大利数学家卡尔丹(Cardan)。在讨论是否有可能将10分成两部分,使两者的乘积等于40时,他指出:这个问题没有任何有理解,然而,如果把答案写成5 square(15)和5-square(15)这样两个怪模怪样的表达式,就可以满足要求了。
既然有人敢把负数的平方根写下来,并且,尽管这有点想入非非,却把10分成两个乘起来等于40的事办成了;这样,有人起了头,负数的平方根—卡尔丹给它起了个非凡的名字叫“虚数(imaginary number)”—被频繁地被科学家们所使用,虽则总是伴有很大保留,并且要提出种种借口。在著名瑞士科学家欧拉(Euler,数神,曾听过高斯讲课)1770年发表的代数著作中,有许多地方用到了虚数。然而,对这种数,他又加上了这样一个掣(che四声)肘的评语:“一切形如square(-1)和square(-5)的数学式,都是不可能有的、想象的数,因为它们所表示的是负数的平方根。对于这类数,我们只能断言,它们既不是什么都不是,也不比什么都不是多些什么,更不比什么都不是少些什么。它们纯属虚幻。”但是,尽管有这些非难和遁词,虚数还是迅速成为分数的根式中无法避免的东西。没有它们,简直可以说寸步难行。不妨说,虚数构成了实数在镜子里的幻想。而且正像我们从基数1可得到所有实数一样,我们可以把square(-1)作为虚数的基数,从而得到所有的虚数。通常写作i(imaginary number)。
虚数闯进数学的领域之后,足足有两个世纪的时间,一直披着一张神秘的、不可思议的面纱。直到两个业余数学家给虚数作出了简单的几何解释以后,这张面纱才被揭去。这两个人是:测绘员威塞尔(Wessel),挪威人;会计师阿尔刚(RobertArgand),法国巴黎人。




依靠(-1)的平方根这个虚数,人们还找到了另一个宝藏,这就是发现普通的三维时间可以和时间结合,从而形成遵从思维几何学规律的思维空间。
,