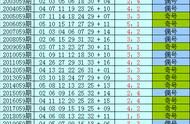
接上文,十位数相同、个位数相加得10的两位数乘法。
这种类型还有第二个类型:两位数平方速算法。

例题:23²=?
1、找出该两位数接近的整十数(基数),算出补数;
如题:23接近10的整数是20,23=20 3
2、将两位数加上补数;
如题:23加上它超出20的数值3,23 3=26
3、将上一步结果乘上整十数(基数)的十位数;
如题:20是10的2倍,将26乘以2,26*2=52
4、算出23超出基数20的数值3的平方;
如题:3²=9
5、因为两位数的底数是10;
如题:52*10 9=529
得出:23²=529

例题:37²=?
1、找出该两位数接近的整十数(基数),算出补数;
如题:37接近10的整数是40,37=40-3
2、将两位数加上补数;
如题:37加上它与40的差值-3,37 (-3)=34
3、将上一步结果乘上整十数(基数)的十位数;
如题:40是10的4倍,将34乘以4,34*4=136
4、算出37与基数40的差值3的平方;
如题:3²=9
5、因为两位数的底数是10;
如题:136*10 9=1369
得出:37²=1369

是不是有点复杂呢,但这个原理还是补数思想的一种延伸,它用10做底数,把两位数的平方运算简化成加减和个位数的平方运算,只要会“九九乘法表”的小朋友,就可以运用这个办法快速地口算出所有结果,再试试吧[机智]
示例:
43²
=【(43 3)*4*10】 3²
=(184*10) 9
=1840 9
=1849
72²
=【(72 2)*7*10】 2²
=5180 4
=5184
两位数的平方一共有81组,很多常见的两位数平方我们都会熟记,遇到不熟悉的数字用这个简化后的算法试试,是不是会提高运算速度呢,可以验证一下哦[玫瑰]
,