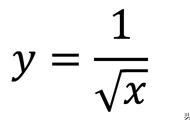例1、求√49的平方根。
分析:这是一种典型的易错题型,许多学生看到这种题的第一反应就是七七四十九,信心满满地写下答案±7(或7),根本就没有看清题意。
本题不是求√49等于多少,而是求√49的平方根,因为√49=7,所以本题的真实含义是求7的平方根,7的平方根为±√7,所以√49的平方根为±√7。
例2、若a没有平方根,且|2a+3|=4,求a的值。
分析:因为负数没有平方根,所以可以得到a<0,故2a+3<3①;
又|2a+3|=4,所以2a+3=±4②。
综合①②可知2a+3=-4,即2a=-7,解得a=-7/2。
例3、已知m^2=16,n^2=25,求
①若mn<0,m+n的值是多少;
②若mn>0,m-n的值是多少。
分析:因为m^2=16,所以m=±4,
n^2=25,n=±5。
①若mn<0,说明m、n异号,所以当m=4时,n=-5;当m=-4时,n=5。故m+n的值为1或-1。
②若mn>0,说明m、n同号,所以当m=4时,n=5;当m=-4时,n=-5。故m-n的值为1或-1。
例4、若3m-5的平方根为±2,4m+3n+6的平方根是±6,求m+n的平方根是多少。
分析:3m-5的平方根为±2,所以3m-5=(±2)^2,即3m-5=4,解得m=3。
又因为4m+3n+6的平方根为±6,所以4m+3n+6=(±6)^2,即4m+3n+6=36,4m+3n=30。
又m=3,所以4×3+3n=30,3n=18,解得n=6。
故m+n=3+6=9。
所以m+n的平方根为:
±√(m+n)=±√9=±3。
例5、若A是一个正数,且A的两个平方根分别为5x-7和3x-17,求A的值。
分析:因为A是正数,正数有两个平方根,且这两个平方根互为相反数,所以5x-7和3x-17互为相反数,即:
5x-7+3x-17=0,8x-24=0,
解得x=3。
A=(5x-7)^2
=(5×3-7)^2
=8^2
=64。
例6、已知M的两个平方根为下列方程:5x+2y+9=0的一组解,求M的值。
分析:因为一个实数的两个平方根是互为相反数的,又该实数的两个平方根是方程5x+2y+9=0的一组解,即该二元一次不定方程的互为相反数的那组解(x=-y)是实数M的平方根。
由题意得:-5y+2y+9=0,
解得y=3。
所以3和-3是M的两个平方根,故
M=(±3)^2=9。
【练一练】
1、求下列各数的平方根。
①√64;
②√(81/16);
③(-3)^2。
2、已知一个自然数的平方根为±m(m>0),那么与其相邻的两个自然数的平方根分别为多少?
3、若x^2=1,y^2=9,且x+y<0,求x-y的值。
4、如果m、n分别是2020的两个平方根,求2020m+2020n+mn的值。
5、若(m^2+n^2+3)^2=25,求m^2+n^2的值。
6、若3-2a与5a+3是正数N的平方根,求N的值。