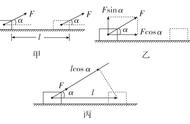
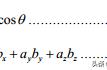我们知道,当力F作用在一个物体上会产生什么样的作用效果呢?
力F作用在某一物体上时,可能会使物体的位移发生改变。
当力F作用在某一个物体上,如果物体在力的方向上发生了位移,或者说,力在物体位移的方向上分力不为零时,我们就可以说,力F对物体做了功。
我们就可以把上述的文字表述理解为功的概念。
不过,我们也可以把力F的功理解为:力F在物体位移s(空间)上的积累效果。
功的计算用公式表示就是:
W=Fscosθ
其中θ是力F与位移s的夹角。
由数学知识我们知道:
当θ角为锐角时,cosθ为正值,那么我们计算出来的结果W就为正。
当力F对某一物体所做的功为正时,可以理解为力F会使物体的速度增加,进而使物体的动能增加。力F对于物体的动能的增加在起正向的作用。
当θ为钝角时,cosθ为负值,那么我们计算出来的结果W就为负。
当力F对某一物体所做的功为负时,可以理解为力F会使物体的速度减小,进而使物体的动能减小。力F对于物体的动能的增加在起负向的作用。
当θ=90度时,力F与位移s垂直,或者说力F与物体速度v的方向始终垂直时,此时,力F不做功。
比如前面我们所学到的匀速圆周运动的向心力是不做功的。
功虽然有正负,但是功是标量,力F所做的功的正负只是表示力F对物体的作用效果是使物体的动能增加还是使物体的动能减小。
所以,当我们求几个力所做的功之和的时候,我们可以把各个力所做的功求出来,之后简单的代数和相加就可以得到这几个力的所做功之和。
那么,接下来我们来介绍下功率的概念。
我们把单位时间内做功的多少称为功率。
或者说功率表示做功的快慢。
所以,我们可以得到功率的计算公式为:
P=W/t=Fs/t=F*v,其中v是这段时间t内的平均速度。
当功率P对应一段时间t时,我们就把P称为力F在该段时间t内的平均功率。
可以想象,当时间t足够短时,上述公式中的平均速度就变成了瞬时速度,那么功率P就从平均功率变成了瞬时功率。
,