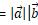向量的基本几何意义
自由向量:
大小和方向(物理:矢量)
向量的数学表示:
把空间中所有的向量的尾部都拉到坐标原点,这样N维点空间可以与N维向量空间建立一一对应关系:N维点空间中点(0,0,0…0)取作原点,那么每一个点都可以让一个向量和它对应,这个向量就是从坐标原点出发到这个点为止的向量。
向量加法的几何意义:
平行四边形法则、三角形法则
向量加法的物理意义:
船过河问题:船头的位移(马达动力)、流水影响的位移(水速)、真正的位移
向量内积:

向量a和b的长度之积再乘以它们之间的夹角的余弦;
向量a和b的坐标分量分别对应乘积的和。
向量内积的几何和物理意义:
向量内积的几何解释就是一个向量在另一个向量上的投影的积,也就是同方向的积
特别的,如果一个向量如a是某个坐标轴的单位坐标向量,那么,两个向量的内积

就是向量b在此坐标轴上的坐标值。这个结论非常重要,这是傅立叶分析的理论基础。
其他几何意义:从内积数值上我们可以看出两个向量的在方向上的接近程度。当内积值为正值时,两个向量大致指向相同的方向(方向夹角小于90度);当内积值为负值时,两个向量大致指向相反的方向(方向角大于90度);当内积值为0时,两个向量互相垂直
向量内积的生活解释:单价向量乘以数量向量,得到总价格
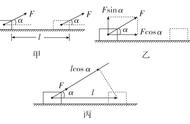
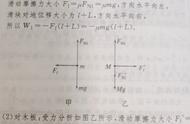
向量内积的物理解释:一个斜坡上用力F斜上拉一个物体,位移为S(没有重力的情况下),那么这个力F所作的功

向量的外积(叉积):