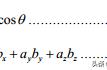空间两条直线用向量计算夹角的方法
近年来高考数学利用向量计算二面角,直线夹角的试题似乎每年都有,这是一种趋势,说明向量计算的简洁和直观。
本篇讲述向量的点积,也叫数量积的计算方法,从而得出向量夹角的公式。
我们知道向量是有大小和方向:

两个向量的乘积可以是个数量,如力在一个方向上作用会使物体在另一个方向移动所做的功,这个积就是向量的点积,有:

为什么乘以余弦,而不是正弦,这是因为力做功只有在移动的方向才有功,垂直移动的方向是不做功的,或做功为零,而力在位移方向的投影就是和余弦相关。
两个向量不管放在哪里,只要大小相等,方向一致,就是一个向量,所以在直角平面坐标系中,某个向量的表达是唯一的,我们沿着x 轴的单位向量为i, 沿着y轴的单位向量为j, 那么向量a可以表示为:

由于单位向量i和j相互成90度,所以i.j=1x1.cos=0,因此: