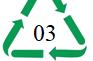
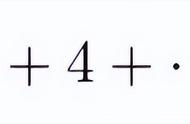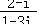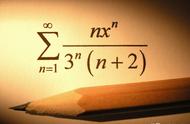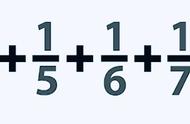, 除以 4得3k 1<M.同样与M是使猜想不成立的最小数矛盾。故M只可能是4k 3形式的数。
再应用数学归纳法知识,由于有验证的基础,我们可以假设猜想对一切小于或等于4k正整数都成立,当n=4k 1时,3(4k 1) 1=12k 4, 除以 4得3k 1<4k,知猜想成立。当n=4k 2时, 除以 2得2k 1<4k,知猜想成立。当n=4k 4, 除以 4得k 1<4k,知猜想成立。故如果能证明n=4k 3时,猜想也成立,根据归纳法原理,知猜想对一切自然数都成立。
结论2:设M是使3n 1猜想不成立的形如4k 3的最小正整数,则


证明:设K=4m时是使3n 1猜想不成立的形如4k 3的整数,3(4k 3) 1=12k 10,除以2得6k 5,3(6k 5) 1=18k 16=72m 16,除以8得9m 2<4k 3=M,M使猜想不成立,故9m 2也使猜想不成立,这与M是使猜想不成立的最小数矛盾。
设K=3m 1时是使3n 1猜想不成立的形如4k 3的整数,则4k 3=3(k 1) K=3(k m 1) 1,故k m 1也使猜想不成立,而k m 1<M=4k 3,这与M是使猜想不成立的最小数矛盾。
设