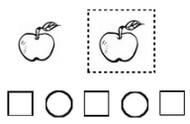
4.机器人从自然数1开始由小到大按如下规则进行染色:
凡能表示为两个不同合数之和的自然数都染成红色,不符合上述要求的自然数染成黄色(比如23可表示成两个不同合数15和8之和,23要染红色;1不能表示为两个不同合数之和,1染黄色).问:要染成红色的数由小到大数下去,第2000个数是多少?请说明理由。
【分析与解】 显然1要染黄色,2=1 1也要染黄色,
3=1 2,
4=1 3=2 2,
5=1 4=2 3,
6=1 5=2 4=3 3,
7=1 6=2 5=3 4,
8=1 7=2 6=3 5=4 4,
9=1 8=2 7=3 6=4 5,
10=1 9=2 8=3 7=4 6=5 5,
11=1 10=2 9=3 8=4 7=5 6。
可见,1,2,3,4,5,6,7,8,9,11均应染成黄色。
下面统一观察其他自然数,说明其他自然数均要染成红色。
1)当n为大于等于10的偶数时,n=2k=4 2(k-2)。
由于n≥10,所以k≥15,k-2≥3,2(k-2)与4均为合数,且不相等。于是,大于等于10的偶数都可以表示两个不同的合数之和,应染成红色。
2)当n为大于等于13的奇数时,n=2k 1=9 2(k-4)
由于n≥13,所以k≥6,k-4≥2,2(k-2)≥4与9均是合数,且不相等.也就是说,大于等于13的奇数均能表示为两个不同的合数之和,应染红色。
所以,除了1,2,3,4,5,6,7,8,9,11这10个数染黄色外,其余自然数均染红色,第k个染为红色的数是第(k 10)个自然数(k≥2)。
所以第2000个染红色的数是2000 10=2010.

5.在整数中,有用2个以上的连续自然数的和来表达一个整数的方法.例如9:9=4 5,9=2 3 4,9有两个用2个以上连续自然数的和来表达它的方法.
(1)请写出只有3种这样的表示方法的最小自然数.
(2)请写出只有6种这样的表示方法的最小自然数.
【分析与解】关于某整数,它的“奇数的约数的个数减1”,就是用连续的整数的和的形式来表达种数。
根据(1)知道,有3种表达方法,于是奇约数的个数为3 1=4,对4分解质因数4=2×2,最小的15(1、3、5、15);
有连续的2、3、5个数相加;7 8;4 5 6;1 2 3 4 5;
根据(2)知道,有6种表示方法,于是奇数约数的个数为6 1=7,最小为729(1、3、9、27、81、243、729),有连续的2,3、6、9、10、27个数相加:
364 365;242 243 244;119 120 … 124;77 78 79 … 85;36 37 … 45;14 15 … 40.

6.从整数1开始不改变顺序的相加,中途分为两组,使每组的和相等.如从1到3的话,1 2=3;从1到20的话:1 2 3 … 14=15 16 17 … 20。
请问:除上述两例外,能够列出这样的最短的整数算式是从1到几?
【分析与解】我们用这种阶梯图来表示连续的数相加,假设情况见下图,

我们通过图得知,c是公共部分,而b c为原等式的右边,a c为原等式的左边,所以有a=b,a部分面积为