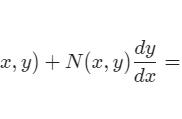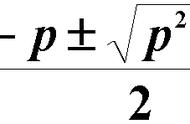2)设a(x)和b(x)在区间α<x<β上连续,则由上述通解公式可知,线性微分方程(1)的一切解在α<x<β上存在,面对非线性微分方程,一般就没有这种解的全局存在性,例如非线性微分方程

关于x的定义域为-∞<x< ∞,而它的解,例如y=tanx的存在区间只是-π/2<x<π/2,这就表明,非线性微分方程解的存在区间一般是局部的,而不像线性微分方程的解那样是全局的。
3)求线性微分方程(1)满足初始条件

的解,由通解,得y(x0)=C,因而再由C=y0,即得初始问题的解为

根据上面的解法可知,这也是唯一的解,这就证明了对于线性微分方程的初值问题,它的解是存在并且唯一的。而对于非线性微分方程的初值问题,它的解有时就不是这样。因此线性微分方程的解在结构上要比非线性微分方程的解简单一些。
举例:设跳伞员的质量为m,降落伞的浮力与它下降的速度v成正比,求下降速度v(t)的变化率。
先取坐标系,参看图2-4,我们规定v正向指向地面,则重力w=mg是正的,而浮力f0=-kv(常数k>0)向上为负,因此跳伞员所受的外力为