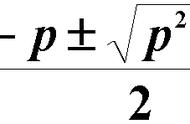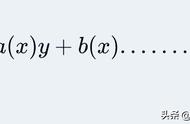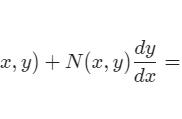成考专升本:二阶常系数线性微分方程的考点!
若函数y₁,y₂为该方程两个线性无关的解,即y₁≠ky₂,则该方程的通解为y=C₁y₁ C₂y₂.
考点2 二阶常系数线性非齐次方程y” py' qy=f(z)解的结构
若y*为方程y” py' qy=f(x)的一个特解,ӯ=C₁y₁ C₂y₂为与其对应的齐次方程y” py' qy=0的通解,则y* y为方程y” py' qy=f(x)的通解.
若y₁是方程y” py' qy=f1(x)的解,y₂是方程y” py' qy=f₂(x)的解,则y₁十y₂是方程y” py' qy=f₁(x) f₂(x)的解.
考点3 二阶常系数线性齐次方程y” py' qy=0通解的求法
先写出与其对应的特征方程r² pr q=0.
1.若特征方程有两个不等实根r₁,r₂,则齐次方程的通解为ӯ=C₁eʳ1ˣ” C₂er₂x.
2.若特征方程有一重根r,则齐次方程的通解为ӯ=(C₁x C₂)eʳˣ.
3.若特征方程无实根,或者说有一对共轭复根r₁=α iβ,r₂=α-iβ,则齐次方程的通解为ӯ=eᵃˣ(C₁cosβx C₂sinβx) .
考点4 二阶常系数线性非齐次方程y” py' qy=f(x)通解的求法
1.先求出与其对应的齐次方程y” py' qy=0的通解y.
2.再求出非齐次方程的特解y*,则该方程的通解为y=ӯ y*.
3.特解y*的求法
(1) 若f(x) =Pn(x) eᵃˣ, 则方程的特解可设为y*=xӯᴷQn(x) eᵃˣ,其中Qn(x)与Pn(x)是同次多项式,系数待定,且
k=0,α不是特征根,
k=1,α为单独特征根,
k=2,α为二重特征根.
(2) 若f(x)=eᵃˣ(Acosβx Bsinβx),则方程的特解可设为y*=xᴷeᵃˣ(A₁cosβx B₁sinβx)。其中A₁,B₁为待定系数,且
k=0,a iβ不是特征根,
k=1,a iβ是特征根.
解题指导
二阶常系数线性微分方程的求解方法:
第一步:首先判断方程类型是否为二阶常系数线性微分方程.
第二步:若是,看是齐次,还是非齐次.
1.若是齐次的,应先写出特征方程:r² pr q=0,然后求特征根,由特征根构造方程的通解.
2.若是非齐次的,应先求出其对应的齐次方程的通解,然后构造非齐次方程的特解,最后由解的结构得到原非齐次方程的通解.
本文来自"四川成人高考网-2020年四川成考网上报名入口”(各搜索引擎搜索“四川成人高考网-2020年四川成考网上报名入口”点击进入网站主页(注意网址中间部分为paccad)查看更多的关于当年成人高考教材大纲、成考招生院校、成考报名时间、成考考试时间、成考成绩查询、成考录取查询、四川成考招生专科、四川成考复习资料等内容;同时还可领取全套的成考教材 试卷)。
,