说起周期问题,相信各位小伙伴应该并不陌生,我们在行测数量关系中经常会见到周期问题,周期问题无论是国家公务员考试或是各地方省考、甚至是事业单位考试,周期问题也都会经常出现,不失为是一个比较热门的一类题型,很多时候各位小伙伴并不是不会做周期问题只不过在做题的时候经常会忽略一些问题,由于马虎而出错。
其实周期问题我们可以用我们学过的计算问题中的公约数和公倍数来解决。我们在学习公约数和公倍数的时候提到过,一般情况下我们研究最大公约数以及最小公倍数,那么对于最小公倍数来说我们该如何应用呢,我们在在这里给大家展示一道典型题供大家参考,希望能对大家有所帮助。
对于周期性问题来说,其实就是各个周期之间的关系的问题。那么具体是什么样的呢,接下来我们就以例题展示的形式给大家做简短的说明。
例:某单位小范,每9天去体育馆打一次羽毛球,老刘每12天去体育馆打一次羽毛球。某天两人在体育馆相遇了,那么下一次他们在在体育馆相遇至少需要过多少天?
A.36天 B.72天 C.90天 D.180天
【答案】A
【中公解析】题目中想求解的是,他们下一次相遇最近的一次时间是几天,在这道题目中提到了小范和老刘他们各自去打羽毛球的一个周期,分别是9天和12天。那么下一次相遇又过了多少天呢?这是一类典型的周期性问题。
我们举个简单的例子,比如小王和小李是室友,小王2天洗一次衣服,小李3天洗一次衣服,某次他们二人周一一起洗了一次衣服,那么我们来思考一下,下一次二人又一起洗衣服是周几?通过列举我们知道小王洗衣服应该是周一下一次是周三、周五、周日这样以此类推按照2天为一个周期进行列举。小李则是周一、周四、周日以此类推按照3天一个周期进行列举。我们发现小李和小王在周日又一起洗衣服了。那么周日这天是在他们周一一起洗衣服之后的第6天。这个6天恰好是2和3的最小公倍数,所以他们下一次相遇的时候恰好是二者周期的最小公倍数。
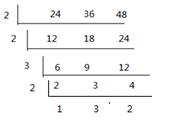
因此我们这道题中,周期分别是9天和12天,那接下来我们找到9和12的最小公倍数36。也就是说再过36天小范和老刘再一次在体育馆相遇打羽毛球了。因此在解决周期问题是通常情况下找下一次相遇至少要过多少天,大家只要去找不同周期的最小公倍数即可。故本题选择A选项。
通过上述简单的题目我们知道周期问题可以通过求解不同周期的最小公倍数即行求解即可,因此我们学习的关于公倍数就可以应用到解决周期问题当中,而对于这样的周期问题呢一般情况下是需要我们去计算最小公倍数
,