来源人们常用‘大海捞针’,‘煎水作冰’ ,‘化圆为方’等成语表示不可能完成的事情。这其中,‘化圆为方’蕴含着丰富的数学知识与数学思想,你知道是什么吗?此外,为什么‘化圆为方’就意味着不可能呢?数学家们又是如何证明其不可能性的呢?下面让我们一起来探究这个有趣的问题。
“化圆为方”最早由古希腊学者阿那克萨哥拉提出,他生活在公元前 5 世纪,在数学和哲学领域都有所贡献。相传他因亵渎神灵被捕入狱,在狱中实在过于无聊,便提出了这么一个作死问题:"怎样作出一个正方形,才能使它的面积与某个已知圆的面积相等?" 这就是化圆为方问题。之所以说这个问题作死,是因为阿那克萨哥拉虽然提出了这个问题,却不能提供参考答案,并且在这之后的 2400 多年里,无数大神们在这个问题上折戟沉沙,铩羽而归。

▲ 阿那克萨哥拉, 前 500 年 - 前 428 年(图自维基)
背景
化圆为方是典型的尺规作图问题。所谓尺规作图(Compass-and-straightedge),就是只准许使用不带任何刻度的直尺和圆规绘制目标图形。 这种苛刻的作图条件使得原本很简单的几何作图中产生了一批著名的数学难题,化圆作方便是其中杰出代表。除此之外,还有三等分角问题和立方倍积问题,它们并列为尺规作图三大难题。
未来还会有另外文章介绍余下两个问题。

▲ 化圆为方:求一正方形,其面积和一已知圆的面积相同(图自维基)
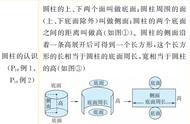
在这里我们有必要先了解下尺规作图,在尺规作图中,直尺和圆规的定义是:
直尺:一侧为无穷长的直线,没有刻度也无法标识刻度的工具。只可以让笔摹下这个直线的全部或一部分。
圆规:由两端点构成的工具。可以在保持两个端点之间的距离不变的情况下,将两个端点同时移动,或者只固定其中一个端点,让另一个端点移动,作出圆弧或圆。两个端点之间的距离只能取已经作出的两点之间的距离,或者任意一个未知的距离。