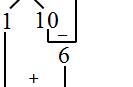定义了直尺和圆规的特性后,所有的作图步骤都可以归化为五种基本的步骤,称为作图公法(The basic constructions):
- 通过两个已知点,可以作出一直线。
- 已知圆心和半径,可以作出一个圆。
- 若两已知直线相交,能够确定其交点。
- 若已知直线和一已知圆相交,能够确定其交点。
- 若两已知圆相交,能够确定其交点。

▲ 作图公法的五种基本步骤
尺规作图研究的,就是是否能够通过以上五种步骤的有限次重复,达到给定的作图目标。尺规作图问题常见的形式是:“给定某某条件,能否用尺规作出某某对象?”比如:“给定一个圆,能否用尺规作出这个圆的圆心?”,等等。
故有:化圆为方问题的完整叙述是: “给定一个圆,是否能够通过以上说明的五种基本步骤,于有限次内作出一个正方形,使得它的面积等于圆的面积”。
如果将圆的半径定为单位长度,则化圆为方问题的实质是作出长度为单位长度√π 倍的线段。
证明要想证明化圆为方的不可能性,即要证明:在尺规作图的条件下,无法作出长度为单位长度√π 倍的线段,这等价于从 1 开始作出 π 。那么,是否可以做出呢?
结合我们所知情况,答案显然是不能。
因为能够用尺规作出的数 z 都有对应的最小多项式,即存在有理系数的多项式 m,使得 m(z)=0。
但对于圆周率 π 来说,这样的多项式不存在(由 1882 年林德曼等人证明)。所以无法用尺规作出数 z=π ,故化圆为方的不可能性得证。
数学上将类似于 这样没有对应的多项式的数称为超越数,有对应的多项式的数称为代数数。
上面关键之处在于林德曼等人的证明,他们用到了现在称为林德曼-魏尔斯特拉斯定理的结论。
相关解法1. 利用密率,近似作图虽然数学家们已经相互独立的证明了超越数不可能由尺规作图构造出来,但这并不影响人类天才解决问题的步伐。下面是一些独特的解法,受过启发的你能不能提出更好的想法呢?
根据前面所讲,化圆为方不可能性的本质在于 π 是超越数,如果将其转换为可用尺规作图方式作出的规矩数 z ,就可以化不可能为可能,解决问题。
沿着这个思路,我们找到了“密率:355/113”,这一关键数。它由中国伟大数学家祖冲之最先发现,是一个与圆周率 π 非常近似且分子分母都是正整数的分数(也就是规矩数,属于代数数),可作出 π 的近似长度。
密率 ,是圆周率比较精确的一个分数近似值。出自《隋书·律历志上》:“密率,圆径一百一十三,圆周三百五十五。约率,圆径七,周二十二。”
主要过程如下: 首先,转换形式:

然后,我们注意到最右边分数,由四则运算和平方构成,符合尺规作图要求,所以我们可将其用尺规作图方法作出来。 尺规作图过程: