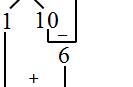这样我们可以在一条直线上画出 AG 3AO 这么长的线段。如下图红线段所示:

接下来我们要作出长度为 √π 的线段: 如上图所示,
- 再在长度为 的线段的右侧同一直线上接上一条长度为 1(也就是 AO)的线段
- 以这两条线段的长度为直线作半圆
- 过这两条线段的交界点作这两条线段的垂线(图中蓝色),与半圆相交
- 根据相交弦定理,交点到直径的距离就为 √π 。
最后:我们就以这条垂线段为一边作正方形。这样,这个正方形的面积就极为近似地等于 π,即等于半径为 1 的圆的面积。 问题解决,利用密率,近似化圆为方!
2. 达芬奇解法上个解法是近似作图,毕竟 355/113 不真等于 π,现在我们跳出尺规作图这个框架,会发现思路开阔许多。
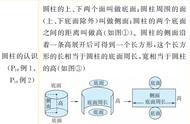
用已知圆为底,圆半径的 1/2 为高的圆柱,在平面上滚动一周,所得的矩形,其面积恰为圆的面积,如图:

证明:

最后,将所得矩形转化为等面积的正方形即可。
这样,化圆为方的问题得到了解决。这种方法由欧洲文艺复兴时期意大利数学家达芬奇提出,所以又称达芬奇解法。当然,这种解法虽然有新颖独特,极易理解等诸多优点,但问题也是存在的。首先是不精确,可操作性不强,所得结果误差较大。其次,违背了题设条件-尺规作图,用了直尺圆规以外的工具,这种开挂操作估计很难让人信服。不过这种从多方面多角度去看问题、分析问题和解决问题的思维方式还是很值得我们认真学习。
结论综上,想必大家对化圆为方问题已经有了大致了解。因为 π 为超越数,无法用尺规作图作出,所以化圆为方为一不可能事件。当然,这是建立在须用尺规作图的条件下,现代计算机借助代数工具已经可以完美地化圆为方,将不可能化为可能,解决了这个千年难题。
那么这几千年来无数英雄好汉前赴后继地研究这个不可能事件是不是就没有意义?显得太傻了呢?通过研究这些几何作图难题,而衍生发展出的尺规作图的判别准则,圆锥曲线研究,进而推动代数数和群论的方程论若干部分的发展,这些对数学发展产生了巨大影响的贡献成果显然不会同意这一观点。
同世间大多事一样,数学的迷人之处从不在于答案,而在于探索问题的过程,解决问题的方法,方法中蕴含的思想,思想里体现的深刻哲理。或许很多时候最后会发现如化圆为方一样是没有答案的,但细细品味整个思维过程产生的一些新思路、新方法和由此派生出的新哲理,你获得的这些早已超越了问题本身,不是吗?
,本文作者:墨水(遇见数学核心成员),喜欢钻进书堆的傻猫一只,爱数学,爱运动,更爱喜欢数学的你们!