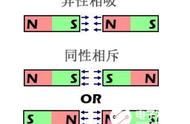
我们知道电荷移动起来就叫电流,有了电流就会产生一个垂直于电荷运动方向的磁场。一根有电流通过的直线导线,就会在电流导线周围产生一个环形磁场,如果我们把载流导线弯成环形或线圈,就会在导线内部产生一个磁场。
也就是说,电流会产生电场,电场会感生出磁性场!那么反过来可行吗?1831年法拉第就发现,如果我们在一个线圈内部施加一个变化的磁场,磁场就会产生电场,电场就会导致线圈中电荷发生移动,并产生电流!这就是电磁感应原理。这也说明了物理定理的对称性。
如果存在磁单极子,麦克斯韦方程则大不相同自然界中可以有电荷,电流和电场,但是就是没有磁荷或磁流,只有磁场。我们可以改变磁场使电荷运动,但不能通过改变电场使磁荷运动,因为根本就没有磁荷。
换句话说,宇宙的电磁特性之间存在着根本的不对称性。这就是为什么“E”和“B”场(电场和磁场)在麦克斯韦方程中的形式看起来也不同。

不用看懂这些方程,我们就能看出电场和磁场方式的不对称,原因是电荷(ρ和Q)和电流(J和I)存在,但与它们对应的磁性物不存在。
但是如果磁荷和磁流确实存在呢?一个多世纪以来,物理学家们一直在思考这个问题,如果磁单极子存在的话,我们可以把麦克斯韦方程的样子写下来,下面是它的微分形式。

左边是之前方程的积分形式,稍微变化了一点;有点是磁单极子存在的方程式。
除了一些基本常数以外,新方程看起来非常对称!我们可以通过改变电场来让磁荷运动,产生磁流。
寻找磁单极子20世纪30年代,狄拉克曾对磁单极子进行过研究,人们当时普遍认为,如果它们真的存在,肯定应该会留下一些蛛丝马迹。但是并没有任何磁单极子存在的证据,也很难通过实验手段去证明它们的存在。
这种情况在20世纪70年代开始发生了稍微的改变。当时人们正在提出大统一理论,或者说是一个认为自然界更为对称的观点。
今天,宇宙的对称性可能被严重的破坏了,导致我们的宇宙有四个独立的基本力,但也许这四种力都以某种高能量统一为一种独特的力?所有这些理论的其中的一个结果都预示着,在标准模型外有新的高能粒子存在,并在许多不同的形式下,磁单极子被预测可能存在。

物理学家一直以来对寻找磁单极子都充满着热情,因为在人们心中有追求对称美的倾向,再加上这些提出的新理论更是引起了人们对寻找磁单极子的兴趣。所以在20世纪70年代,人们一直在寻找它们,最著名的一次实验是由布拉斯·卡布雷拉的物理学家领导的实验。他用一根长金属丝绕了八个环路线圈,这样就能测量通过金属丝的磁通量。如果一个磁单极子通过了线圈,就会得到正好八个磁单极子的信号。但如果是一个标准的磁偶极子穿过线圈,就会得到一个 8信号紧接着是一个-8信号,这样就能把单极子和偶极子区分开来。