平行四边形面积等于两倍的三角形面积,即:

那么棱柱体的体积为:

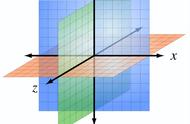
这个结果和行列式的计算结果是一样的。根据上面的两个例子,我们可以粗略地(因为没有严格证明)下一个结论:行列式的计算结果即是对应向量所围合的空间体量。这一点在对角行列式上最明显,每个维度上,只有一个非零数值,截取三维空间上的一部分,恰好是一个立方体。
这样我们就好理解,为什么行列式要斜着相乘了。因为不同维度相乘才对其空间体量有意义,这就好比求面积要长X宽,求体积要长X宽X高。
至于行列式各项的乘积法则反而不重要,因为我们不需要每项都算。回头看上面的行列式计算,行列式变换前后是等价的,所以我们可以把行列式化简到最简单的形式,再计算。

基于上述的内容,有下面几个结论:
1、一个行列式可以有无穷多种变形,对应的无穷多的向量空间在体量上是等价的。就像水一样,在不同的容器里,形状会变,体积不变。
行列转置也是变形的一种,不影响计算结果。
2、行列式可以提取公约数,对应的向量空间体量等比例缩小,从图形上大约也能看出来,如下图: