本节虽然是以三种投资品进行实验,但是它的结论可以推广到多个投资品中,对实际投资进行指导(实际投资中投资品个数往往超过三个)。
可以看到,仅在非常严苛的假设下,原始的 EWRCP 风险平价问题才等价于最大化投资组合的夏普率。然而在实际中,我们几乎无法保证投资品的夏普率相同以及它们收益率之间独立或相关系数相同。因此从业务上说,拿来一个协方差矩阵就按照 EWRCP 问题一通优化,得到的最优资产配置很可能没有任何业务道理。
这是否意味着 EWRCP 模型在实践中没有用呢?答案是否定的。下面就来看看如何用 EWRCP 模型实现风险平价的本质理念。
5 用 EWRCP 实现风险平价的本质通过上面的分析我们知道,在实际中直接套用 EWRCP 的数学模型时,应该考虑以下两点:
- 如果已知不同投资品的夏普率(可以用历史数据估计或者由因子法推断等),那么应该按照夏普率的平方分配风险,即考虑 SSWRCP 模型。
- 在输入代表风险的协方差矩阵时,应该忽略收益率之间的相关性、仅输入一个对角矩阵 —— 对角线上的第 i 个元素代表第 i 个投资品的风险。如果不忽略收益率之间的相关性,EWRCP 模型得出的最优资产配置权重往往缺乏业务含义。(顺便提一句,桥水并不是使用历史收益率的波动率来衡量投资品的风险,那么做实际上非常粗糙且不准确。桥水从对经济的理解出发来预测不同类的投资品的风险(Hoffstein 2012)。)
上面的第二条往往令人费解。桥水的全天候投资组合中,恰恰利用的就是不同投资标的在不同的经济环境表现的负相关性 —— 比如在经济增长时股票表现好、债券表现差。那么为什么我们要在 EWRCP 中忽略收益率之间的相关性呢?这里的门道在哪呢?
正确的答案是这样的。
协方差矩阵中的相关系数是投资品之间的序列相关性,它描述的是两个投资品的收益率各自围绕其均值波动的一致性程度;而反观桥水经济四象限中的投资品,它们的负相关性体现在不同经济环境下收益率均值的负相关性,这和上述序列相关性毫无关系。
比如在经济增长时,股票的收益率均值可能是 8%,而债券的收益率均值是 -3%,它们的收益率均值呈负相关,但这两个投资品的收益率序列各自围绕 8% 和 -3% 波动,而这两个波动之间一定会有某种序列相关性。如果不加忽视,这个相关性就会作为 EWRCP 模型的输入 —— 协方差,从而对最优解造成影响。从风险平价的本意来说,这个序列相关性是不应该被考虑的。因此,在用协方差矩阵作为 EWRCP 模型的输入时,应该忽略不同投资品收益率之间的协方差,而仅考虑每个投资品自己的方差。
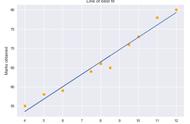
6 实证本节通过一个简单的实证说明正确和错误的使用 EWRCP 模型将产生千差万别的影响。考虑四个代表性的投资品:美国 7 – 10 年国债(IEF)、沪深 300 指数(A)、标普 500 指数(SPX)以及黄金(GLD)。实证的时间区间为 2009 年 1 月 31 日至 2017 年 11 月 30 日。这段时间内这些投资品的风险收益情况如下表和下图所示。


首先,我们来看错误考虑收益率之间序列相关性的情况,即我们把收益率的协方差矩阵直接带入到 EWRCP 模型中。为了比较,我们使用资金等权的配置作为基准(通过杠杆把两个组合的月收益率的波动率控制在 4%)。这两种方法都是按月再平衡,它们的最优资产配置权重及对应的投资组合效果如下所示。
令人意外(or 不出意外,毕竟我们错误的使用了 EWRCP 模型!)的是,错误风险平价模型的计算结果仅仅保证了数学上这四个投资品(在错误的考虑了序列相关性时)对投资组合有相同的风险贡献,而其组合的实际收益情况非常差(它竟然做空标普 500 指数,这从业务上丝毫没有逻辑),在测试期内年化收益率为负。