运筹学数学规划模型分为哪两种,运筹学模型总结

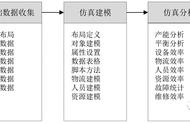
每一个程序员或开发者都会面临着如何提升系统吞吐量、如何减少系统访问耗时尖刺、如何机器CPU利用率、如何降低系统响应时间、如何减少系统内存占用等问题。通常情况下，我们会分析系统JVM参数、埋点查看耗时模块、优化网络访问方式、优化序列化或压缩方案、数据编码等等方案解决以上的问题。

但是如果站在更高的层次上，可以看出我们实际面临的问题一个如何更好的管理我们所拥有的的计算资源，以最大程度的利用计算资源的问题，想到这一层，很容易会联想到本专题的主题运筹学，正所谓夫运筹帷幄之中，决胜千里之外。

本文作为【程序员学习运筹学】的开篇，首先会介绍下什么是运筹学，让我们一起走进它。

运筹学一次最早起源于20世纪30年代。《中国大百科全书》的释义为：运筹学是“是用数学方法研究经济、民政和国防等部门在内外环境的约束条件下合理分配人力、物力、财力等资源，使世纪系统有效运行的技术科学，它可以用来预测发展趋势，制订行动规划和优选可行方案。”

运筹学一词在英国称为operational research，在美国称为operations research，可以直译为“运用研究”或“作业研究”。由于运筹学涉及的主要领域是管理问题，研究的主要手动是建立数据模型，并比较多的运用各种数学工具。从这点触发，有人将运筹学称为“管理数学”。1957年我国从“夫运筹帷幄之中，决胜千里之外”（见《史记高祖本纪》）这句古语中摘取“运筹”二字，将 O.R.正式译为运筹学，包含运用筹划，以策略取胜等意义，比较恰当地反映了这门学科的性质和内涵。

所谓系统就可以理解为是由相互关联、相互制约、相互作用的一些部分组成的具有某种功能的有机整体。

运筹学研究中不是对各个子系统的决策行为孤立评价，而把有关子系统相互关联的决策结合起来考虑，把相互影响和制约的各个方面作为一个统一体，从系统整体利益触发，寻求一个优化协调的方案。

一个组织或系统的有效管理涉及很多方面，运筹学研究中吸收来自不同领域、具有不同经验和技能的专家。由于专家们来自不同的学科领域，具有不同的经历和经验，增强了发挥小组集体智慧、提出问题和解决问题的能力。这种多学科的协调配合在研究的初期，在分析和确定问题的主要方面，在选定和探索解决问题的途径时，显得特别重要。

为制定决策提供科学依据是运筹学应用的核心，而建立模型则是运筹学方法的精髓。学习运筹学要掌握的最重要技巧就是提高运筹学数学模型的表达、运算和分析能力。

任何一门学科从研究范畴上大致都可分为以下四个方面：

1. 从观察现象所得到的的结果和进行这种观察所需要的特殊方法
2. 理论或模型的建立
3. 将理论与观察相结合，并从结果得到预测
4. 将这些预测同新的观察相比较，并加以证实

运筹学也不例外，主要包括以下6个步骤，这些步骤往往需要交叉反复进行。因此在运筹学的研究中，除对系统进行定性分析和收集必要的资料外，一项主要的工作是努力建立一个用以描述现实世界复杂问题的数学模型。这个模型是近似的，它既精确到足以反映问题的本质，又粗略到能够求出数量上的解。

任何决策问题进行定量分析前，首先必需认真地进行定性分析。

1. 确定决策目标，明确主要要决策什么，选取上述决策时的有效性度量，以及在对方案比较时这些度量的权衡。
2. 辨认哪些是决策中的关键因素，在选取这些关键因素时存在哪些资源或环境的限制。

模型是对现实世界的事物、现象、过程和系统的简化描述，或其部分属性的模仿，是对实际问题的抽象概括和严格的逻辑表达。建立模型的好处：

1. 使得问题的描述高度规范化，掌握其本质规律。
2. 建立模型后，可以通过输入各种数据资料，分析各种因素同系统整体目标之间的因果关系，从而确定一套逻辑的分析问题的程序方法。
3. 建立系统的模型，为应用电子计算机来解决问题架设起桥梁。

一般建立模型时应尽可能选择建立数学模型，即用数学语言描述的一类模型。但有时问题中的各种关系难以用数学语言描绘，或问题中包含的随机因素较多，也可以建立起一个模拟的模型，即将问题的因素、目标及运行时的关系用逻辑框图的形式表示出来。

用数学方法或其他工具对模型求解。

根据问题的要求，可分为别求出

• 最优解
• 次优解
• 满意解

依据对解的精度的要求及算法上实现的可能性，又可以分为

• 精确解
• 近似解

将实际问题的数据资料代入模型，找出精确的或近似的解，这解毕竟是模型的解。

为了检验得到的解是否正确，常采用回溯的方法，即将历史的资料输入模型，研究得到的解与历史实际的符合程度，以判断模型是否正确。

• 当发现有较大误差时，要将实际问题同模型重新对比，检查实际问题中的重要因素在模型中是否已考虑，检查模型中各公式的表达是否前后一致。
• 当输入发生微小变化时，检验输出变化的相对大小是否合适，当模型中各参数取极值时，检验问题的解，还要检查模型是否容易求解，并在规定时间内算出所需的结果等，以便发现问题，对已构建的模型进行修正。

任何模型都有一定的使用范围，模型的解是否有效，要首先注意模型是否继续有效，并依据灵敏度分析的方法，确定最优解保持稳定时的参数变化范围。一旦外界条件参数变化超出这个范围时，及时对模型和导出的解进行修正。

需要明确：

1. 方案由谁实施
2. 什么时间实施
3. 如何实施
4. 要求估计实施过程可能遇到的阻力
5. 指定相应的克服困难的措施

运筹学按所解决问题的性质的差别，将实际的问题归结为不同类型的数学模型。这些不同类型的数据模型构成了运筹学的各个分支。

当变量连续取值，且目标函数和约束条件均为线性时，称这类模型为线性规划模型。线性规划建模相对简单，有通用算法和计算机软件，是运筹学中应用最为广泛的一个分支。有些规划问题的目标函数是分线性的，但往往可以采用分段线性化等方法，转化为线性规划问题。

如线性规划模型中目标函数或约束条件不全是线性的，对这类模型的研究构成非线性规划分支。

线性规划和非线性规划两类模型中变量的取值必须为整数时，粉白构成线性整数规划或非线性整数规划。整数规划中有一类变量取值为0或1，称为0-1整数规划模型，它对应的方案的“舍”或“取”，对问题的建模起了特殊作用。

上述三类规划模型中，均为在满足一组约束条件下追求单一目标的优化。实际问题中往往需要对多个目标进行优化，且这些目标间既在优化方向上存在矛盾，又缺乏公度性，无法综合成统一目标，因此导致目标规划分支的诞生。

动态规划是研究多阶段决策过程最优化的运筹学分支。即从系统化总体出发，要求各阶段所构成的决策序列使目标函数值达到最优。

运筹学中把一些研究的对象用节点表示，对象之间的联系用连线（边）表示，点、边的集合构成图。图论是研究由节点和边所组成图形的数学理论和方法。图是网络分析的基础，利用图论方法来研究各类网络结构和流量的优化分析，网络分析还包括利用网络图形来描述一项工程中各项作业的进度和结构关系，以便对工程进度进行优化控制。

存储论是一种研究最优存储策略的理论和方法。存储策略研究在不同需求、供货及到达方式等情况下，确定在什么时间点及一次提出多大批量的订货，适用于订货、储存和可能发生短缺的费用的总和为最小。

排队系统由服务机构（服务员）及被服务的对象（顾客）组成。排队论研究顾客不同输入、各类服务时间的分布、不同服务员数及不同排队规则情况下，排队系统的工作性能和状态，为设计新的排队系统及改进现有系统的性能提供数据依据。

• 一般顾客的到达及服务员用于对每名顾客的服务时间是随机的，服务员可以是一个或多个，多个情况下又分为平行和串行排列。
• 排队按一定规则进行，一般按到达顺序先到先服务，但也有享受优先服务权的。
• 按系统中顾客容量，可分为等待制、损失制、混合制等。

对策论用于研究具有对抗局势的模型。在这类模型中，参与对抗的各方称为局中人，每个局中人均有一组策略可供选择，当各局中人分别采用不同策略时，对应一个收益或需求支付的函数。

对策论已应用于商品、消费者、生产者之间的供求平衡分析，利益集团间的协商和谈判，以及军事上各种作战模型的研究等。

决策是指为最优地达到目标，依据一定准则，对若干备选行动的方案进行的抉择。即实行科学的决策程序，采用科学的决策技术和具有科学的思维方法。决策过程一般是指：

1. 形成决策问题，包括提出方案，确定目标及效果的度量
2. 确定个方案对应的结局及出现的概率
3. 确定决策者对不同结局的效用值
4. 综合评价，决定方案的取舍

决策论是对整个决策过程中涉及方案目标选取、度量、概率值确定、效用值计算，一直到最优方案和策略选取的有关科学理论。

一般认为运筹学诞生的三个来源是军事、管理和经济，但其中管理是运筹学孕育的主要土壤，因为基于军事和经济研究中产生的运筹学方法或分支最终都移植到管理中应用和发展。

随着生产规模的日益扩大和分工的越来越细，要求生产组织高度的合理性、高度的计划性和高度的经济性，促使人们不仅研究生产的各个部门，而且要研究他们相互之间的联系，要当作一个整体研究，最求整体的效率和效益，这正是运筹学研究的基础和目标。

运筹学的诞生既是管理科学发展的需要，也是管理科学研究深化的标志。可以方便的解决管理中的库存问题、系统排队优化问题、通过编制网络计划从系统的观点揭示了工序间的联系和制约。运筹学应是数学这个学科中同管理联系最紧密的部分。

运筹学在管理人才的培养中占有十分重要的地位。

1. 有助于训练管理人员的逻辑思维能力，辨别问题中的可控因素和非可控因素，弄清问题的要素结构及其相互联系。
2. 有助于培养管理人员对问题的直觉洞察和全局分析能力，当面对一个问题时能很快的对该问题作出一个大概的判断，以致预见到问题的可能结局。

运筹学应用软件的开发是同运筹学的发展紧密相连的。因为即使是一个只含有几十个到上百个变量的线性规划模型，通过手工求解十分繁杂甚至不可能。而实际问题的数学模型要远远复杂的多，变量个数甚至多达几十万个、上百万个，因此必须要借助计算机软件进行求解。

目前国内常用的求解运筹学模型的软件主要包括LINDO、LINGO、WinQSB、Matlab等。

互联网企业为节省成本，一般会选择相对价格低廉的计算机，将众多的计算机组合排列后通过集群的形式对外提供互联网访问支持。我们可以将众多的计算机想像成被管理的资源。那么，运筹学上的绝大部分数据模型都可以应用到对互联网架构或系统的优化中。

• 排队论，可以用来优化微服务RPC的访问策略，可以用于优化系统内部多线程。
• 图论与网络分析，可以用于优化任务调度策略。
• 线性规划、非线性规划、整数规划、目标规划，可以用于优化系统资源的使用，降低系统运行费用成本。
• 存储论，可以用于优化私有云的机器上限或下限、也可以用于优化系统内存使用。
• 对策论，可用于优化流处理系统化中如何控制生产者和消费者的供求平衡关系问题、也可以优化计算机CPU中生产者消费者模型的平衡关系，以最大的提升CPU的使用率。