怎么证明五角星180度,五角星角度计算方法

沉迷数学的史蒂文又来啦！欢迎和我一块学习。

「图解数学」系列，根据欧几里得几何推演逻辑，用学生看起来最为直观的图形，来讲解平面几何各个知识点。

连载12期，精确覆盖 SAT/ACT 平面几何部分的所有考点；涉及 AMC 8 和公立学校初中平面几何重要知识点，并为国际学校和公立学校学生作中英文对照。

AMC 的全称是American Mathematics Competitions，美国数学竞赛。有三种等级： AMC 8 / AMC 10 / AMC 12，分别对应不超过 8/10/12 年级的学生参加，美国及其他地区均可参加。

需要详细了解的您可以看：

下面进入正文部分：

01

“人伸开双臂的长度基本等于人的身高”，像这样一句话，在数学里就叫做命题（statements）了，有好奇者想检验这句话的真伪，“论证这句话是对的”的过程就叫做命题的证明。在真实的英文数学考题中，会有“Show that ...” “Prove that ...”之类的题目。

数学中的证明基本可以分为两种：

这种证明的基本逻辑是用具体案例套“大前提”，“大前提”一般是已知的定理。比如咱们上期讲到的“三角形内角和是180°”这个定理，如果在某个题目中，一个复杂的图形中存在三角形DEF，那么DEF就是具体案例，立即能推出 ∠D ∠E ∠F=180°。

比如想证明下图中最后一步的结论，∠4=∠1 ∠2，可以由三角形内角和是 180° 计算 ∠1 ∠2=180°-∠3，由平角性质计算 ∠4=180°-∠3。两个式子算出同样的结果，说明两个式子一样，即 ∠4=∠1 ∠2，这就是平面几何中的一个重要性质：

三角形一个外角等于不相邻的两个内角和。

02

在我讲平面几何过程中，听到很多来自学生的疑惑：那些奇奇怪怪的辅助线 （guideline）谁能想到？想不到这条辅助线这题是不是就做不了了？

事实上，不做辅助线也会有其他方法做，只不过做辅助线会大大简化证明过程，所以希望大家在平时学习中，积累一些常见的辅助线的作法，辅助线不是说谁能在考场瞬间想到的，考场的成功都来自于平时的厚积薄发。

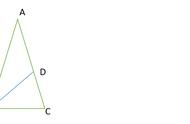
比如，已知下面右图中∠1，∠2，∠3各多少度，求∠4的大小。可做一条辅助线，把图形拆分成两个三角形，连用两次上面所说的重要性质“三角形一个外角等于不相邻的两个内角和”。可得出结论：

凹四边形凹角等于其余三个角之和。

这就是辅助线的作用：把不熟悉的东西转化成熟悉的。辅助线的本质是连接已知条件，用虚线搭建桥梁。

03

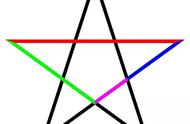
我记得我小时候，特别羡慕班里会徒手画五角星（pentagram）的人，我学了一下怎么一笔画如下图的五角星，然而画的很歪。后来学了几何知识才知道，无论画的五角星是正的还是歪的，它五个角之和永远都是180°！

想想怎么证明这个有趣的性质吧，可以参考下图。