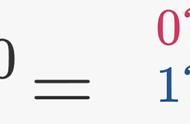在数学世界中,每个运算及其结果都有一个非常合理的解释,因为数学是建立在非常简单且本质上是防弹原理的基础上的。如果我们改变其中的一些原则,我们最终会得到一个结果,即坚如磐石的数学基础经历了有趣的蜕变。
许多学生在他们的数学教育中一遍又一遍地重新学习相同的原理。然而,他们往往经常听到一件事,那就是“你永远不能将一个数除以零”。一旦他们进入高中,他们就会听到“一个数字除以零会产生不确定的结果”这句话。几乎每天。

虽然一开始用数字除以零似乎很基本,但它并不是那样工作的。假设我们要思考一下这个概念。在那种情况下,我们注意到围绕它思考变得越来越复杂。因为数学家还没有有效地定义数字除以零的结果,所以它仍然是未定义的。对于许多人来说,数字除以零的结果缺乏定义仍然很难处理。
但是像数学这样的理性概念怎么能不定义这么简单的操作呢?
首先,在将数字除以零之前,我们需要假设我们知道如何计算加法和减法。为了更好地理解任何数学数字的除法,我们可以按以下方式处理这个问题:
例如,让我们将数字 1 除以非常接近于零的数字。
1/0.1等于10.
1/0.01等于100.
1/0.001等于1000.
1/0.0001等于10000。1/0.00001等于100000. 1/
0.000001等于1000000.1/0.00000000.1
/0.0000001等于10000000. 1/0.0000000001等于100000000.1/1/1/1/1/1
/1
/1/
1/ 0.000000001 等于 1000000000。1
/0.0000000001 等于 10000000000。1
/0.00000000001 等于 100000000000。1
/0.000000000001 等于 1000000000000。
如果我们走得更远,我们会更接近于零,例如将 1 除以 0.0000000000000000000001,我们得到 10000000000000000000000(Septillion)。所以我们用来除 1 的数越接近零,结果就越大,这是一个清晰的模式。
那么如果我们采用逻辑的方式,用1除以0不应该得到无穷大的结果吗?虽然一开始看起来在理性上直截了当,但当除数接近零时结果接近无穷大与简单地假设 1 除以零是无穷大是不一样的。一方面,我们接近;另一方面,我们断言是这样,但为什么呢?
当人们进行此类查询时,我个人很喜欢。
要理解这个问题,我们首先要知道除法是什么意思。如果我们举一个简单的例子,数字 10 除以数字 5 表示需要添加多少个数字 5 才能达到数字 10。那么,换句话说,五乘以什么得到 10?
如果我们详细检查这个例子,我们会注意到一些事情;除数意味着做乘法的逆运算。所以这意味着如果我们可以将任何给定数字乘以另一个数字“x”,这意味着我们可以将最终结果相乘得到原始数字的结果。如果我们能找到这样一个数,则称为该数的乘法逆元。
这方面的一个例子是,当你将 2 和 3 相乘时,你会得到 6。这意味着要再次得到 3,你需要将 6 乘以 ½。所以 2 的乘法逆元是 ½。使用这些值,我们可以得到另一个有趣的结果。
一个数乘以它的逆元总是等于 1。
这意味着如果我们将一个数除以零,零也需要有一个乘法逆元,它需要是 1/0。此外,当我们将 1/0 乘以 0 时,我们应该得到 1。但是,根据定义,任何数字乘以零始终为零。所以零没有乘法逆元。
那么我们得到的答案是照顾事情吗?如果我们回到过去,我们可以找到一些数学家改变规则的案例。很久以前,负数没有平方根。后来数学家把它定义为“复数”下的虚数“i ”,从而开创了一个全新的数学世界。
那么,数学家不能再次更改规则并发明一个新规则,将 1/0 定义为无穷大吗?让我们试试吧。
假使,假设;
1/0 = ∞
根据定义,一个数乘以它的乘法逆元必须等于 1。因此无穷大乘以零必须为 1。
0 x ∞ = 1
所以零乘以无穷加上零乘以无穷等于 2。
(0 x ∞) (0 x ∞) = 2
如果我们使用分配属性,零加零乘以无穷大就是 2。对吧?
(0 0) x ∞ = 2
因为零加零等于零,所以它等于零乘以无穷大可以这样写。
0 x ∞ = 2
然而早些时候,我们假设零乘以无穷大等于一。
所以现在我们以 1 等于 2 结束。我们没有在我们的操作中犯任何错误;我们只是得到了一个不正确的结果。如果我们接受这个结果是正确的,我们就会接受数字 1 在数学上等于所有其他数字。这将意味着我们所知道的所有代数的终结。
我对零的力量和奥秘的兴趣是在我读完查尔斯·塞夫 (Charles Seife) 令人难以置信的书《零:一个危险想法的传记》后开始的。它很可能是很长一段时间以来最流行的数学书籍。读完这本大开眼界的书后,我对为什么需要承认零的独特意义有了新的认识。没有它,我们作为一个物种所创造的许多东西将不复存在。这本书值得任何热爱数学或想探索更多数字历史的人阅读!