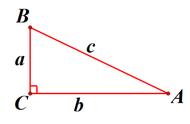
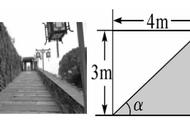
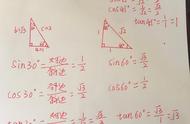三.有三角函数值不能直接利用时作垂线
3.如图,在△ABC中,点D为AB的中点,DC⊥AC,sin∠BCD=1/3,求tanA的值.

【分析】条件有sin∠BCD=1/3,但没有∠BCD所在的直角三角形,无法利用,但已知DC⊥AC,且D为AB的中点,通过倍长中线或作垂线都能构造含∠BCD的直角三角形,如图,过点B作BE⊥CD,交CD的延长线于点E,

∵点D是AB的中点,∴AD=BD,又∠ACD=∠BED=90°,∠ADC=∠BDE,∴△ACD≌△BED,∴CD=DE,AC=BE,在Rt△CBE中,sin∠BCE=BE/BC=1/3,∴BC=3BE,由勾股定理得,CE=2√2BE,∴CD=CE/2=√2BE=√2AC,∴tanA=CD/AC=√2.
四.求非直角三角形中角的三角函数值时构造直角三角形
4.如图,在△ABC中,AB=AC=5,BC=8,若∠BPC=1/2∠BAC,求tan∠BPC的值.

【分析】∵AB=AC=5,BC=8,则等腰△ABC是确定的,又∠BPC=1/2∠BAC,我们就想到过点A作AE⊥BC于E,如图,(利用三线合一)