阿基米德使用微积分作为一种前所未有的简单思维方式。另一方面,理查德·费曼认为微积分是上帝在创造这个宇宙时使用的语言。 实际上,两者都是正确的。微积分不仅是一种思维方式,也是一种解释未知事件的方法。如果我们进一步研究它,我们可以假设它们是同一件事。毕竟,语言是思想的口语形式。(让我们忽略那些不假思索的人)。
自从莱布尼茨向世界提出微积分以来,数学家和物理学家都将微积分应用于他们认为真实但无法证明的物理定律。除此之外,那些掌握数学思维的人,总是用微积分的基础——数学思维来解决身边的复杂问题。
因此毫不夸张地说,我们周围的任何事物都与微积分有关。
微积分处理不断变化的事物。更具体地说,微积分分析不断变化,帮助我们更有远见地行事。它还可以帮助我们找到最佳解决方案来解决因不断变化而出现的问题。
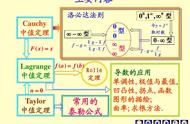
我们今天使用和教授的微积分分为两个主要分支:微分学和积分学。这两个人就像对立的兄弟姐妹。那是因为如果你先求一个函数的导数,然后再求它的积分,你就会回到开始的地方。

微分学处理变化率的概念。这意味着它可以帮助我们找到给定时间范围内的瞬时变化。
例子包括不断变化的东西,我们需要制作图表。血压、心率、股票市场、火箭的重量、跑步者的速度、气压和温度以及细菌数量是许多重要示例中的一部分。在分析曲线图或抛物线时,我们使用微积分来映射这些事件以找到瞬时速率。这意味着如果我们将抛物线放大到足够远并看到一条直线,我们就可以找到平均值或斜率。一个例子是,如果你看 Usain Bolt 跑步的照片,你看不到他在跑步。不过,很明显,他在跑。我们使用微积分来计算他在那个确切实例中运行的速度(瞬时速率)。
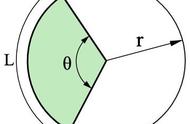
然而,在积分学中,我们找到两个确定点之间的弯曲区域。任何小学生都可以计算正方形的面积。然而,要找到弯曲部分的面积,我们必须将图形分成尽可能多甚至无限多的矩形。之后,我们找到并将所述矩形的面积加在一起,以找到对该部分面积的非常准确的估计。
在本文中,我将讨论微积分的应用,这是我研究了很长时间并在上面尝试简化的主题。我想提一下,在撰写本文时,我从Ali Nesin和Steven Strogatz等不可思议的数学家的讲座中受益匪浅。用我自己的话来说,我将尝试与您分享他们在课堂上教给学生的例子。

事实上,林肯对欧几里德几何原本的痴迷是我们如何将数学应用于现实世界的完美例子。在理论教育体系中,如果一位教师教会学生如何将他们学到的东西与现实世界联系起来,那么他们就被认为是成功的。换句话说,如果学生能够认识到他们在现实世界中学到的东西,那么它在他们的脑海中就会占有更有意义的位置。
作为一名数学老师,当我了解到这种方法时,我被迷住了。自人类被创造以来,每一位数学家和物理学家都应用数学来理解和教导他人我们生活的世界、我们的宇宙,甚至他们所信仰的上帝。古希腊人对几何的好奇源于他们努力理解这个宇宙和上帝创造了它。如果我们从这个角度来看,我们可以假设人类在几千年前就想出了正确的教育体系。更进一步,我们可以假设今天的数学和物理教师是幸运的。