介绍一个数学中非常有趣,有点搞笑又有点意外的问题:稀疏尺问题。

这里的“稀疏”是指尺子的刻度稀疏。你有没有想过,一把尺子上的刻度中,有很多是不必要的。
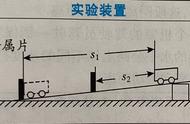
比如,一把长 10 厘米的尺子,如果只要求量出整数厘米的长度,那么这把尺就只需要在 0,1,3,7,8,10 厘米处,这 6 个位置有刻度可以了。

如果要量 1 厘米的长度,就把被测物体放在 0 和 1 两个刻度之间。量 2 厘米,那么就是 1 和 3 两个刻度之间。需要量 3 厘米时,可以把被测物体放在 0 和 3 刻度之间,也可以放在7 和 10 厘米刻度之间,这样就得到了 3 厘米。
量 4 厘米的话,可以把被测物体放在 3 和 7 厘米之间;5 厘米的话,放在 3 和 8 厘米之间等等。请自行验证,用以上这样一把尺子,可以量出全部的,1 到 10 厘米的整数长度。
这把尺子刻度虽然“稀疏”,但确实是一把合格的尺子。能够看出,问题的要点在于,对任何一个被测的整数,需要找到两个数字,使得它们的差等于这个数字。当然,我们希望刻度越稀疏越好,因为刻度越多越没有难度,不稀奇嘛。
那我们可以在脑子里,构造另一个长度的稀疏尺,来加深一下理解。比如,我们要构造一把长度为 9 的稀疏尺,需要量出 1 到 9,所有的整数长度,最少需要几个刻度?这里我省略单位了,因为无关紧要。
首先,传统上我们把 0 也作为一个刻度,总是需要的。另外,可以确定 9 这个刻度也是需要的。因为尺子总长度规定为 9,那么必须有 9 这个刻度,才能量出 9 这个长度。那么,其他刻度的话,哪些需要呢?我们可以可以推演一下。
首先,“1”这个刻度,要还是不要?相信多数读者会选择要。因为我们总需要量出“1”这个长度。否则你需要有另外两个相邻刻度才能解决的问题。所以,看起来,“1”加进来总没错。
那么“2”这个刻度,要还是不要?你可能认为不要“2”,要“3”更好。因为,有“3”的话,“1”和“3”就能量出 2,并且“3”也顺便把自己解决了。
但有“2”这个刻度的话,它也顺便解决了“7”这个长度。因为“2”和“9”之间距离为 7。如果把“2”跳过,那么“7”或“8”就变成必须的了,因为只剩下“0”和“7”或者“1”和“8”之间之间能量出“7”。
到这里,事情开始变得的无比复杂了。光用脑子想,已经很难想清楚了。所以,你可能会想用编程来解决。但对稀疏尺问题来说,用蛮力搜索的难点在于指数爆炸,即需要枚举的可能性太多,以至于等不到出结果的那天。
比如,对特定长度l的稀疏尺,进行编程搜索的话,你是想从刻度数从最多往下减还是最少往上加呢?如果我们希望得到刻度数最少的结果,感觉上从少往上增加比较划算。
但也不用从 1 个刻度开始搜索。因为我们知道条 n 刻度的话,它们的两两组合有 种可能。所以,我们从使得 的那个 n 开始搜索。
比如,长度 l=10 时,可以发现至少需要 5 条刻度。另外,0 和 10 这两个刻度是必须的,所以可以从 1 到 9,共 9 种可能的刻度中,取 3 个数字,有 84 种组合。
然后对每一种组合,你需要两两匹配,再检查匹配的两个数字的差是否覆盖 1 到 9 所有的数字,这本身又是一个计算量很大的过程。
如果 84 种组合都不行,你就需要增加一个刻度,改为搜索 9 个数字里取 4 个数字的组合,有 126 种可能等等。
当然,对长度为 10 的问题,电脑的计算能力没有任何问题。但是,如果长度达到几百以后,需要搜索的组合数是以指数方式增加的,电脑枚举法就很快失效了。后面我们会看到,人类已经构造出来的最长的稀疏尺长度仅为 213。
到此,已经可以看出,对这个稀疏尺问题,其概念非常简单,但无论是推理法还是电脑蛮力搜索都有困难,那么这道题目就有意思了。这里留个思考题,请你设计一把刻度最少的,长度为 9 的稀疏尺(答在文中)。
以下会介绍一下,目前关于稀疏尺问题,人类都知道了些什么结果。但我先得定义几个概念,这几个概念也是帮我们理清思路的一个过程。
(需要注意的是,因为这个问题在数学中比较冷门,不同的文章所定义的名词和概念都有所不同。以下介绍的定义取自 Wolfram 公司的研究员 Ed Pegg Jr.在Hitting All the Marks: Exploring New Bounds for Sparse Rulers and a Wolfram Language Proof[1] 一文中所使用的概念。在其他文献中,请自行甄别术语的定义,可能会有所不同。)
第一个概念,尺(ruler):本文所说的尺,就是 0 到 n 之间的整数的子集,其中包括 0 和 n,因为我们需要量出“1”到“n”这 n 个长度。并且我们说,这把尺子的长度是 n。
第二个概念:完全(complete)尺:这把尺可以量出 0 到 n 之间,所有的整数长度,没有遗漏。
第三个概念:最小完全尺( minimal complete ruler):长度为 n 的完全尺中,刻度最少那把尺。任何长度下,总有 1 把或几把最小完全尺。最小完全尺,是长度一定的情况下,刻度最稀疏的完全尺,所以也简称它为“稀疏尺”(Sparse Ruler)。本文后面提到的稀疏尺,都是最小完全尺。
第四个概念:最优尺(optimal ruler)。它的意思是,在刻度数量确定的情况下,长度为最长的完全尺。稀疏尺是长度确定,刻度最少。那现在固定刻度数,我们能设计出最长的完全尺有多长呢?
此时最长的完全尺,就叫它最优尺,因为它是这个刻度数量下最长的尺了。再增加长度的话,刻度数肯定要增加。可以想见,肯定有些稀疏尺不是最优尺。即可以增加这把尺子的长度,但是不增加刻度数量的情况。
最后一个概念:完美尺(Perfect Ruler)。它是稀疏尺,且比它长的稀疏尺中,没有比它的刻度数更少的了。粗听这个概念有点多余,只有一种情况下,稀疏尺可能不是完美尺,那就是长度增加后,尺子的刻度变少了,这可能吗?这里先买个关子,后面会看到一个非常意外的情况。
定义过这些名词后,我们可以回顾一下关于这个问题研究的历史。稀疏尺问题的研究历史上发生了很多趣事和让你意外的地方。

(长度 10 以内的稀疏尺刻度位置表。Length 是长度,Marks 是刻度数,Number 是数量,Wichmann 是威克曼公式)
首先,关于稀疏尺问题,匈牙利的数学家保罗·埃尔德什(Paul Erdős,1913-1996)就研究过。