图四:黑色的圆代表总只数,红色的点代表假设兔子的脚数,绿色的线代表比实际脚多的6只脚去掉
第四步:因为假设全是兔子后,求出的总脚数要多于实际的脚数。那么,就要把多的这些脚去掉,让4只脚变成2只脚。因为一共多了6只脚,所以,每只兔子的4只脚都要去掉2只脚,也就是求6只脚中有多少个2只?去掉多的脚后,变成2只脚的就是鸡。
多的脚数÷(每只兔子的脚-每只鸡的脚)=鸡子的只数
列式:6÷(4-2)=3(只)(如图四所示)
8-3=5(只)
即:兔子有5只,鸡有3只。

图片来源于人教版四年级下册
其实,鸡兔同笼的问题,如果出现在高年级,是一个很好解决和理解的问题。可以用家长们都学过二元一次方程解决。
三、二元一次方程方法例如:笼子里有若干只鸡和兔,从上面数,有8个头,从下面数有26只脚。鸡和兔各有多少只?
第一步:读题找出已知条件
8个头表示鸡和兔子共8只,总共26只脚,鸡2只脚,兔子4只脚。
第二步:假设鸡有a只,兔子有b只。
a b=8(只)
2×a 4×b=26(只)
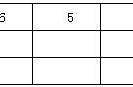
然后,只要解方程式就可以求出鸡和兔子各有多少只。(如图5所示)

图五
不同年级,对学生的要求不同,讲法也就不一样。为什么不能在四年级的时候用方程解决“鸡兔同笼”的问题?
因为教学要尊重孩子的发展规律,这涉及到儿童的发展心理学。现在很多家长辅导作业崩溃的原因就是把家长把自己的思维模式强加给孩子,可是孩子根本不懂。
孩子6个月时,你跟他玩遮挡的游戏,他会笑。这是因为此时他还没有推理能力,他认为他看不见的东西就是不存在的。因此,他看到这个遮挡动作,就像成年人看到一个孙悟空一下出现在面前一样,他当然就笑了。
但孩子2岁时,那在这样,他就不笑了,因为他开始有推理能力了。所以,孩子的推理能力是逐步发展的。

图片来源于网络
著名的发展心理学家皮亚杰教授,最早发现了人类认知发展的规律,按照他的观点,在进入青春期之后,少年的思维才会进展到“形式运算”阶段,他们有了抽象思维的能力。
比如鸡兔同笼的问题,小学生解决这个问题,要用假设法,列表法,抬腿法,但是不能用二次元方程式解决。