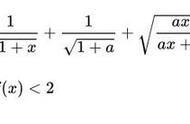1637年的一个深夜,法国图卢兹的一所公寓内,费马正伏案阅读古代数学家丢番图的著作《算术》,看到一个平方数可以写成两个平方数之和,马上联想到一个立方数是否可以写成两个立方数之和?那么n次幂呢,他不由自主地写下了形如方程:Xⁿ Yⁿ=Zⁿ,是否有正整数解?
费马停下了笔,凝视着窗外明亮的月光,进入沉思。忽然,他从椅子上跳了起来,手舞足蹈地喊道:“我知道答案了。”
随即,费马在丢番图译本的空白处写道:我已经想到了一个绝妙的证明,可惜书的空白处不够大,不足以把证明过程写下来。
这便是数学史上著名的费马大定理的由来,具体来说就是:当n>2,方程Xⁿ Yⁿ=Zⁿ没有正整数解。

一、费马的故事
在开始介绍费马大定理之前,先简单介绍一下费马的经历。
费马1601年出生于法国一个叫博蒙-德洛马涅的小城,父亲多米尼克·费马是一个皮鞋商人,母亲是一个议会法官的女儿。优越的出身让费马早年衣食无忧,并受到了良好教育。
费马三十岁时在图卢兹就职,任晋见接待官,同年他与表妹路易丝结婚并生下三个儿子。1648年费马又升任图卢兹地方议会的议员,他在这个岗位上干了十七年,于1665年1月在该城去世,终年65岁。
费马原本是一位律师,他却在数学上取得了非凡的成就,号称业余数学家之王,他是如何兼顾工作和业余两不误的呢?
一位法国评论家给出了答案:费马担任议员的工作对他的智力活动有益无害。议院评议员与其他公职人员不同,对他们的要求是:避开他们的同乡,避开不必要的社交活动,以免他们在履行职责时行贿受贿。
正因为如此,费马在繁重的工作之余, 把研究数学当作一种消遣。谁知,无心插柳柳成荫,费马深陷其中不可自拔,每当他发现一个新的公式,解决一道数学难题时,便欣喜若狂,快乐得像一个小孩子似的。
费马在数学上的贡献是巨大的,在微积分、数论、代数、光的折射原理等各个领域均有建树,尤其是费马大定理的提出,让费马名声大噪,并步入最伟大的数学家行列。

二、一场数学接力赛
费马大定理犹如一座巍峨的山峰,350年来,后世最一流的数学家都向它发起冲锋,均铩羽而归。
1753年,瑞士数学家欧拉用无穷递降法证明了n=3、4时费马大定理成立;
1816年,有人请德国数学家高斯解答费马大定理,高斯研究了一番后深感为难,回复别人说:费马大定理是一个孤立的命题,我对此没有兴趣,因为我可以随手写出无数类似的命题,既不能证明,也无法否定;
1825年,德国数学家狄利克雷和法国数学家勒让德各自独立地证明了n=5时费马定理成立;
1850年,高斯的学生,德国数学家库默尔运用“理想素数”的理论,一下子证明了小于100以内除37、59、67以外的所有奇素数,费马大定理均成立;
库默尔之后,费马大定律的研究工作陷入停滞不前。
德国富豪沃尔夫斯凯尔年轻时为情所困,打算自*。当他拿起匕首时,忽然看到桌子上库默尔的证明,便情不自禁地拿起笔开始计算。哪知,他深陷其中不可自拔,以至于忘记了自*的事情。
后来,沃尔夫斯凯尔重新振作,并成为大富豪。临终前,他立了遗嘱:凡在100年内能证明费马大定理的人,将获得100000马克奖金。

沃尔夫斯凯尔数学奖
从这以后,成千上万的人开始向这一难题发起挑战,很多人宣称证明了费马大定理。经过数学机构的审核,这些证明无一例外都是错误的。
1900年,德国数学家希尔伯特在世界数学大会上对20世纪的数学进行了展望,提出了23个数学难题,其中第十个问题便是费马大定理。有人让希尔伯特攻克这一难题,希尔伯特却说:“我为何要*死一只会下金蛋的鹅呢?”
时间又过了二十年,1922年,英国数学家莫德尔从拓扑学的角度提出了一个著名的猜想:莫德尔猜想。1983年,德国数学家法尔廷斯证明了这一猜想,从而为费马大定理的解决提供了一把钥匙。
1955年,日本数学家谷山丰发现椭圆曲线与有理数域上的模曲线存在某种联系,进而提出了著名的谷山-志村猜想。后来有数学家指出,若能证明谷山-志村猜想,则费马大定理成立。