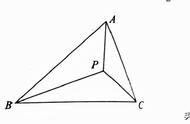
问题:在直线l上找一点P,使得的值最大
解析:连接AB,并延长与1交点即为点P.
证明:如图,根据△ABP
三边关系,BP-AP< AB,即PB - PA< PB – PA。
应用举例例1、如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为____________.

解析:如图,取AB的中点E,连接OD、OE、DE,
∵∠MON=90°,AB=2 , ∴OE=AE=1/2AB=1,
∵BC=1,四边形ABCD是矩形,∴ AD=BC=1, ∴DE=√2,
根据三角形的三边关系,OD<OE DE,
当OD过点E时最大,最大值为√2 1.故答案为:√2 1.
变式1.如图,∠MON=90°,边长为2的等边三角形ABC的顶点A、B分别在边OM,ON上当B在边ON上运动时,A随之在边OM上运动,等边三角形的形状保持不变,运动过程中,点C到点O的最大距离为 ______ .

【解析】如图,取AB的中点D,连接OD、CD,
∵△ABC是等边三角形,∴CD=√3/2×2=√3,
∵∠MON=90°,∴OD=1/2AB=1/2×2=1,
由图可知,当点O、C、D三点共线时点C到点O的距离最大,
最大值为√3 1.故答案为:√3 1.
变式2.(2018•洪泽区一模)如图,在△ABC中,∠C=90°,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点的最大距离是 .

【解答】解:如图,取CA的中点D,连接OD、BD,