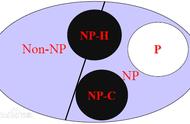
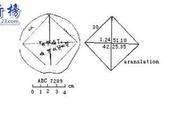
再说一遍,每天都会遇到一个问题。似乎很难——解开这个结?但是,计算此任务所需的最短时间是数学的另一个基石。困难在于我们知道可以计算解耦算法,但它的复杂性可能使得即使是最强大的超级计算机也需要太长时间。
2011 年,美国数学家格雷格·库珀伯格 (Greg Kuperberg) 迈出了解决这个问题的第一步。在他的工作中,解开 139 个顶点的结构 108 小时缩短到 10 分钟。结果令人印象深刻,但这只是一个特例。目前,有几十种不同效率的算法,但没有一种是通用的。该数学领域的应用包括生物学,特别是蛋白质折叠过程。
最大的红衣主教
最大的无穷大是什么?乍一看,这是一个妄想的问题,但它确实是 - 所有无穷大的大小都不同。或者更确切地说,就幂而言,因为这就是数学中区分数字集的方式。基数被理解为集合中元素的总数。例如,最小的无穷大是自然数 (1, 2, 3, ...) 因为它只包括正整数。这个问题目前还没有答案,数学家们不断地寻找越来越强大的集合。
集合的幂的特征在于它的基数,或简称为基数。有一个完整的在线百科全书,其中包含以乔治·康托 (Georg Cantor) 命名的无穷大和著名的“四肢”。这位德国数学家是第一个发现无数集合可以比彼此更大或更小的人。而且,他能够证明不同无穷大的威力差异。
π 和 e 之和有什么问题?
这两个无理数之和是代数数吗?数百年来,我们一直在使用这些常量,但我们从未了解它们的所有内容。代数数 - 具有整数系数的多项式的根。乍一看,似乎所有实数都是代数的,但不是,恰恰相反。大多数数是超越数,也就是说,它们不是代数数。此外,所有实数超越数都是无理数(例如 π 和 e),但它们的和可以是任意的。