圆锥曲线的光学性质和它们的切线方程其实是同一个问题。
因为一个曲面的光学性质,肯定和曲面的法线有关。
光线在曲面某一个点的反射方向,取决于曲面在这个点的法线,法线两侧的入射角和反射角是相等的;曲面上点的法线,又必然和曲面上这个点的切线相互垂直的,就比如下面这种例子:

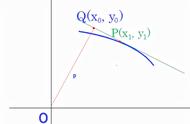
如图光线的箭头所示:如果有一束光从椭圆的焦点射出至P点,这束光的反射光线,一定会指向椭圆的另外一个焦点。
如果想要证明这个结论,必须先把曲面在P点的切线方程写出来,然后才能得到P点的法线方程,如果这条法线PA,能平分焦点三角形两条光线的夹角,那么我们上面的结论就是正确的。
所以第一步要做的就是求曲面在P点的切线方程。
我们可以设出点P 的坐标,根据点斜式写出它的方程,然后把这个方程和椭圆的方程联立。
因为切线和椭圆曲线只有一个交点,那么这个联立的方程只会有一个解。
椭圆在P点处的切线方程:

这个方程的长相和椭圆方程差不多,只不过使用点的坐标代替了其中的一个变量而已。
上述求椭圆切线方程的方法很传统,是最常用的一种,推导过程计算量很大,需要很好的多项式的化简功夫和恒等变形的能力,但好在它的思路清晰,大多数同学们都能想到,而且细心点也能做到很完美,所以,我依旧推荐这种方法,虽然很笨,但符合常规思维,适合大多数学生。
一旦推导完成一次以后,你就可以直接使用上述结论,而无需再次推导。
也就是说,你可以在考试中,直接使用上述公式对付圆锥曲线试题中,那些不需要写出解题过程的选择题和填空题,也可以在大题中首先采用上述结论得出最终的切线方程,得出这个最终结论之后,再返回头,装模作样地把假设的切线方程和圆锥曲线方程联立,省略中间的计算过程,直接写出你刚才已经得到的答案就可以。这样做一来可以提高解题效率,节省时间,二是可以避免因为过程缺乏而造成的扣分。
现在我们得到了p点切线的斜率:

我们就可以知道P点的法线PA的斜率: