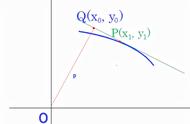
我们就可以写出法线的方程,然后求出A点的坐标。、
在焦点三角形中,我们只需证明这条法线就是这个三角形的角平分线就ok,此时只需证:

各个点的坐标现在都很明确,所以,剩下的就是极具耐心地计算了(此处省略)。
这就是椭圆曲线的光学性质:在椭圆中,通过一个焦点发出的光线,经过椭圆曲线的反射后,反射光线必定经过另一个焦点。
这其实也是这两个定点被称为焦点的根本原因。
除了椭圆之外,双曲线、抛物线都具有类似的光学性质,如图:

上图中,从双曲线一焦点发出的光线,经过双曲线反射后,反射光线的反向延长线,必定经过双曲线另外一支的焦点。

抛物线的反射特性更有特点,从它焦点发出的光线,经过抛物面反射后,反射光线会平行于抛物线的对称轴。
人教版教材中拿出很大一部分笔墨,专门讲解了三大圆锥曲线的光学性质,但只是要求如何使用这些性质即可,对数理上的验证并没有提出很高的要求,所以,如果这些知识点出现在考试题目中,难度也不会太高,对学生还是相对友好的。
在《白话高中数学》这个系列里,到今天为止,已经把向量、直线和圆,椭圆、双曲线和抛物线等解析几何部分的知识点以及考点聊的差不多了,这部分文章的全文,都是首发在同名“深度一佳”公众号上的,公众号头像也和这儿一样,为了方便部分家长,我还做了合集PDF打印版,感兴趣的朋友可以搜索公众号深度一佳查看。以后再讨论这一部分知识的话,估计就要做真题解析了,欢迎大家继续关注。