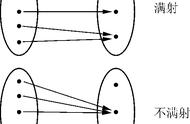
康托集合论的提出,数学家认为数学大厦已经建成数学可以定义为这样一门学科,我们永远不知道其中所说的是什么,也不知道所说的内容是否正确。 ——罗素
从古希腊先哲中诞生的“极限”和“无理数”两头恶兽,曾经引发了第一次数学危机和第二次数学危机,什么是“极限”?从古希腊数学家芝诺开始,人类就一直在思考无穷小量究竞是不是零?无穷小及其分析是否合理?这让数学家十分痛苦,即使过了2000多年,牛顿的微积分依然深陷于“极限”的泥沼之上。

“阿基里斯追不上乌龟”:阿基里斯总是首先必须到达乌龟的出发点,因而乌龟必定总是跑在前头。这是对“极限”难题的形象诠释之一。
正如希尔伯特说的那样:“没有任何问题象无穷那样深深地触动人的情感,很少别的观念能象无穷那样激励理智产生富有成果的思想,然而也没有任何其它概念能象无穷那样需要加以阐明”。
而无理数则把希腊先哲创立的“万物皆为数”的世界击垮,古希腊人把有理数视为连续衔接的那种算术连续统的设想彻底地破灭了,人类转而开始探索集合。

这也让数学的发展一直摇摇欲坠,这两把悬在所有数学家头上的利剑在肆虐了2000年之后,威尔斯特拉斯、狄德金和康托等人发起了浩浩荡荡的分析算术化运动,建立了完备的实数体系,将“极限”、“无理数”两头恶兽斩*,从而为数学的发展铺平了道路。

当时,康托尔和戴德金都是将实数定义为有理数的某些类型的“集合”。戴德金方法可以称为序完备化方法,康托尔方法可以称为度量完备化方法。这些方法在近现代数学中都已成为典型的构造方法,被后人不断推广发展成为数学理论中的有力工具。