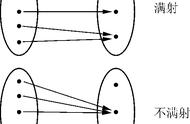
这就是数学史赫赫有名的“一个理发师冲进了大厦,把整个大厦搞了个天翻地覆,甚至直接动摇了整个数学大厦的地基”事件。
理发师引发的第三次数学危机将数学界搞得所有数学家都焦头烂额,直因为罗素悖论只涉及最基本的集合论概念:集合,元素,属于和概括原则,它的构成十分清楚明白,所以它涉及的是数学基础问题。
这个悖论的出现说明以往的朴素集合论中包含矛盾,因而以集合论为基础的整个数学就不能没有矛盾。这个悖论也同时说明数学中采用的逻辑也不是没有问题的。
罗素悖论表明不能无条件承认概括原则,然而概括原则的改变将使集合论大为改观,因此对整个数学的影响是巨大的。简单来说,承认无穷集合,承认无穷基数,看起来悖论可以消除,矛盾可以解决,然而数学的确定性却在一步一步地丧失。这就是问题的矛盾所在。

这也让许多毕生从事集合论的数学家难以接受,甚至许多成果都付之一炬,数学家弗雷格在他刚要出版的《算术的基本法则》第2卷末尾写道:
"一位科学家不会碰到比这更难堪的事情了,即在工作完成之时,它的基础垮掉了,当本书等待印出的时候,罗素先生的一封信把我置于这种境地"。
这就是真理的无穷,即使我们对于数学大厦的构建耗费了如此巨大的精力,花费了数千年的时间,我们得出的很多结论仍然不是严密的,可能会有漏洞。
为了解决危机,1908年策梅洛提出了比较完整的公理,这些公理指明了对集合的哪些操作是合法的。后经过弗兰克尔的完善和补充,形成了ZF公理系统。
(ZF1)外延公理:一个集合完全由它的元素所决定。如果两个集合含有同样的元素,则它们是相等的。
(ZF2)空集合存在公理:即存在一集合s,它没有元素。
(ZF3)无序对公理:也就是说,任给两个集合x、y,存在第三个集合z,而w∈z当且仅当w=x或者w=y。
(ZF4)并集公理:也就是说,任给一集合x,我们可以把x的元素的元素汇集到一起,组成一个新集合。
准确的定义:“对任意集合x,存在集合y,使w∈y当且仅当存在z使z∈x且w∈z”。
(ZF5)幂集公理:也就是说,任意的集合x,P(x)也是一集合。
准确的定义:“对任意集合x,存在集合y,使z∈y当且仅当对z的所有元素w,w∈x”。
(ZF6)无穷公理:也就是说,存在一集合x,它有无穷多元素。
准确的定义:“存在一个集合,使得空集是其元素,且对其任意元素x,x∪{x}也是其元素。”
根据皮亚诺公理系统对自然数的描述,此即:存在一个包含所有自然数的集合。
(ZF7)分离公理模式:“对任意集合x和任意对x的元素有定义的逻辑谓词P(z),存在集合y,使z∈y当且仅当z∈x而且P(z)为真”。
(ZF8)替换公理模式:也就是说,对于任意的函数F(x),对于任意的集合t,当x属于t时,F(x)都有定义(ZF中唯一的对象是集合,所以F(x)必然是集合)成立的前提下,就一定存在一集合s,使得对于所有的x属于t,在集合s中都有一元素y,使y=F(x)。也就是说,由F(x)所定义的函数的定义域在t中的时候,那么它的值域可限定在s中。
(ZF9)正则公理:也叫基础公理。所有集都是良基集。说明一个集合的元素都具有最小性质,例如,不允许出现x属于x的情况。
准确的定义:“对任意非空集合x,x至少有一元素y使x∩y为空集。”
这在一定程度上解决了第三次数学危机,但是却并没有彻底将理发师从数学大厦当中请出去,长达100多年的数学危机如今还没有解决。
矛盾的消除,危机的解决,往往给数学带来新的内容,新的进展,甚至引起革命性的变革,这也是危机带给数学界最大的意义。

我们也期待数学家有一天可以真正解决第三次数学危机,甚至建立起一座新的数学大厦。