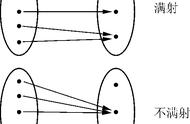
康托尔的有理数序列理论
而康托尔的这些思想也促进了集合论的诞生。1873年11月29日康托尔给戴德金写了一封信,把导致集合论产生的问题明确地提了出来:正整数的集合(n)与实数的集合(x)之间能否把它们一一对应起来。同年12月7日,康托尔写信给戴德金,说他已能成功地证明实数的“集体”是不可数的,也就是不能同正整数的“集体”一一对应起来。这一天应该看成是集合论的诞生日。
集合论是研究集合(由一堆抽象物件构成的整体)的数学理论,包含了集合、元素和成员关系等最基本的数学概念。
而集合论中元素也有三大特性:确定性、互异性、无序性。首先集合中的元素必须是确定的,例如{我们学校帅的男生}这就不是一个集合,因为帅的定义不同,有些人认为阳刚是帅,有些人认为阴柔是帅,所以元素不确定;集合中的元素必须是互不相同的 ,例如{5,6}是一个集合,但是不能表示为{5,6,5},这就是互异性;{1,2,4}和{4,2,1}是同一个集合,这就是集合的无序性,因为集合中的元素是不存在顺序的。
从1879年到1883年,康托尔写了六篇系列论文,论文总题目是“论无穷线形点流形”,其中前四篇同以前的论文类似,讨论了集合论的一些数学成果,特别是涉及集合论在分析上的一些有趣的应用。第五篇论文后来以单行本出版,单行本的书名《一般集合论基础》。第六篇论文是第五篇的补充。《一般集合论基础》在数学上的主要成果是引进超穷数。
该文从内容到叙述方式都同现代的朴素集合论基本一致,所以该书标志着点集论体系的建立。康托尔创立的集合论可以说在数学的发展中起到了重大的作用,在数学中占有一个独特的地位,它的基本概念已渗透到数学的所有领域。

数学家们发现,从自然数与康托尔集合论出发可建立起整个数学大厦。因而集合论成为现代数学的基石。
这让数学家欢喜异常,1900年国际数学家大会上,法国著名数学家庞加莱就曾兴高采烈地宣称:“……借助集合论概念,我们可以建造整个数学大厦……今天,我们可以说绝对的严格性已经达到了……”。

庞加莱的话反而成了一个Flag,在两年之后,罗素在集合论中发现了一个问题,罗素是著名的哲学家、文学家、数学家,他擅长从哲学的角度去思考数学的发展,也就是我们经常说的“数学是什么”这一高度去看待数学。
1903年,罗素从集合元素的三大特性中发现了康托尔集合论中的一个BUG。罗素设集合S是由一切不属于自身的集合所组成,即“S={x|x ∉ S}”。那么问题是:S包含于S是否成立?首先,若S包含于S,则不符合x∉S,则S不包含于S;其次,若S不包含于S,则符合x∉S,S包含于S 。根据排中律,一个元素或者属于某个集合,或者不属于某个集合。因此,对于一个给定集合,问是否属于它自己是有意义的。但对这个看似合理的问题的回答却会陷入两难境地。

而罗素悖论影响最广的版本就是“理发师悖论”:在某个城市中有一位理发师,他的广告词是这样写的:“我只给所有不给自己刮胡子的人刮胡子”。
来找他刮脸的人络绎不绝,这些人自然都是那些不给自己刮脸的人。可是,有一天,这位理发师从镜子里看见自己的胡子长了,他本能地抓起了剃刀,你们觉得他能不能给他自己刮脸呢?
如果他不给自己刮脸,他就属于“不给自己刮脸的人”,他就要给自己刮脸,而如果他给自己刮脸呢?他又属于“给自己刮脸的人”,他就不该给自己刮脸。