一个例子假设检验是推断统计的一项重要内容,现实生活中有大量的事例可以归结为假设检验问题。
由统计资料得知,1989年某地新生儿平均体重为3190克,现从1990年新生儿中随机抽取100个,测得其平均体重为3210克,问1990年的新生儿与1989年相比,体重有无显著差异?

从调查结果看,1990年的新生儿的平均体重比1989年新生儿的平均体重增加了20g,但是这20g的差异可能是由于抽样的随机性造成的,也可能是1990年新生儿体重确实比1989年新生儿体重有所增加。
下面采取假设检验的方式来解决这个问题。
假设1989年和1990年新生儿的体重没有显著差异,再利用1990年新生儿体重的信息检验该假设是否成立,如果成立,说明这两年新生儿的体重没有显著差异,反之,说明1990年新生儿的体重确实比1989年有显著增加。
假设检验基本原理1、假设表达式
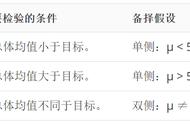
在统计学中,采用一个等式或不等式表示问题的原假设。在新生儿体重这个例子中,原假设为:

备择假设:如果原假设不成立,就要拒绝原假设,在另一个假设中做出选择,这个假设称为备择假设。在新生儿体重这个例子中,备择假设为:

说明:
- 原假设一般用H_0表示,备择假设用H_1表示。
- 原假设与备择假设互斥,接受原假设,就意味着放弃备择假设,拒绝原假设,则表示接受原假设。
- 在某些文献中,备择假设(alternative hypothesis)也成为替换假设。
2、两类错误
对于原假设提出的命题,需要做判断,如果原假设正确,则接受原假设,反之,则拒绝原假设,当然,这是依据样本的信息做出的判断,实际情况并非如此,所以判断有可能正确,也可能不正确。
我们可能犯的错误有两种类型:
第I类错误:原假设为真,却被我们拒绝,犯这种错误的概率用a表示。
第II类错误:原假设为假,我们却没有拒绝,犯这种错误的概率用β表示。
假设检验中各种可能性结果的概率如下。