假设检验的流程
1、提出假设:原假设和备择假设
2、确定适当的检验统计量
3、根据显著性水平,进行统计决策
例如,针对上述新生儿体重问题:
1、提出假设:原假设和备择假设
原假设:

即1989年和1990年新生儿体重没有显著差异
备择假设:

即1989年和1990年新生儿体重有显著差异
2、确定适当的检验统计量
确定检验统计量主要根据2点:样本量的大小和总体标准差是否已知。

这里100个新生儿,属于大样本,应该使用z统计量。
说明:统计学中,一般样本量大于30,即可认为是大样本。
3、根据显著性水平,进行统计决策
这里假设显著性水平为0.05,总体标准差为80。
这里提到的显著性水平,其实就是上面提到的两种错误中的第I类错误。
经过计算,z值为2.5,临界值为1.96。
可以看出,z值大于临界值,所以z值落入拒绝域,所以拒绝原假设,即认为1989年和1990年新生儿体重有显著差异。
关于z值及临界值计算的说明:
z值根据公式计算即可,在Excel输入公式:=(3210-3190)/(80/10)
临界值:=NORM.S.INV(1-0.05/2)
假设检验的方向性1、双侧检验
上面提到的新生儿问题,原假设表示等于,备择假设表示不等于,这种属于双侧检验。
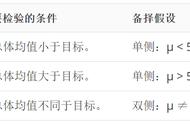
2、单侧检验
还有一些假设问题,带有方向性,根据方向分为两种:左单侧检验和右单侧检验。
- 例如,灯泡的使用寿命、轮胎行驶的里程数,所考察的数值越大越好,这种属于左单侧检验。
- 例如,废品率、生产成本,所考察的数值越小越好,这种属于右单侧检验。
对于单侧检验,假设表达式可能会有大于或者小于的情况: