统计学中,我们关心的统计量一般有三个:均值、比例和方差,把问题分成两类。
一个总体参数的假设检验一个总体参数的假设检验有三种类型。
1、总体均值的检验
2、总体比例的检验
3、总体方差的检验
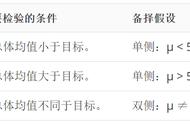
这三种类型的假设检验对应的统计量及公式如下。

一个关于总体均值的假设检验问题:
例题:某批发商欲从厂家购进一批灯泡,根据合同规定灯泡的使用寿命平均不能低于1000小时。已知灯泡燃烧寿命服从正态分布, 标准差为200小时。在总体中随机抽取了100个灯泡, 得知样本均值为960小时, 批发商是否应该购买这批灯泡?
1、提出假设:原假设和备择假设
H0:μ≥1000
H1:μ<1000
2、确定适当的检验统计量
这里100个灯泡,属于大样本,选择z统计量。
3、根据显著性水平,进行统计决策
这里假设显著性水平为0.05,根据公式计算z值为-2。
计算临界值为,1.64。
|-2|>1.64,所以z值落入拒绝域,拒绝原假设,即批发商不应该购买这批灯泡。
关于z值及临界值计算的说明:
z值根据公式计算即可,在Excel输入公式:=(960-1000)/(200/10)
临界值:=NORM.S.INV(1-0.05)
这里需要注意:
两个总体参数的假设检验单侧检验,临界值计算公式为:
=NORM.S.INV(1-0.05);
双侧检验,临界值计算公式为:
=NORM.S.INV(1-0.05/2)(之前的新生儿体重问题属于双侧检验,所以用这个公式计算临界值)。
有时候,我们可能需要比较两个总体的参数,例如,在相同年龄的情况下,学历对职工的收入是否有显著的差异。
两个总体参数的检验也有三种类型。
1、两个总体均值之差的检验
2、两个总体比例之差的检验
3、两个总体方差比的检验
这三种类型的假设检验对应的统计量及公式如下。

一个关于两个总体均值之差的假设检验问题:
尽管存在争议,但大多数科学家认为,食用含有高纤维的谷类食物有助于降低癌症发生的可能性。然而有一个科学家提出,如果人们在早餐中食用高纤维的谷类食物,那么平均而言,与早餐没有食用谷物的人群相比,食用谷物者在午餐中摄取的热量(大卡)将会减少(Toronto Star, 1991)。如果这个观点成立,谷物食品的生产商又将获得一个很好的机会,他们会宣传说:“多吃谷物吧,早上也吃,这样将有助于减肥。”为了验证这个假设,随机抽取了35人,询问他们早餐和午餐的通常食谱,根据他们的食谱,将其分为两类,一类为经常的谷类食用者(总体1),一类为非经常阅类食用者(总体2)。然后测度每人午餐的大卡摄取量。经过一段时间的实验,得到的结果如表8—3所示。

试以α=0.05的显著性水平检验。
本题要检验的命题:早餐食用较多的谷类食物有助于减少午餐中热量的摄取。
1、提出假设:原假设和备择假设
H0:μ_1-μ_2≥0
H1:μ_1-μ_2<0
2、确定适当的检验统计量
这里是小样本,而且总体标准差未知,所以选择t统计量。
3、根据显著性水平,进行统计决策
这个问题属于双样本异方差的情况(题目中没有明确说方差相等,所以认为方差不等),选择对应的公式计算即可。