层次分析法。
发酵的海绵。
40岁的富婆、27岁的知心姐姐,还有18岁的俏皮妹妹,到底该选哪个?这个问题困扰我们许久,索性就在今天做个了断。
先根据自身喜好选择一个,可以是三秒内的一见钟情,也可以是暂停后的深思熟虑。这个无伤大雅,主要是与最终结果做个对比。
今天用到的分析工具是层次分析法,简称AHP,是美国运筹学家萨蒂提出的。它将多目标决策问题看作为一个系统,通过对目标构成的要素进行分解,从而在多种方案中找出决策的最优解。
它在生活与工作中得到广泛应用,如营销策划哪个更适合的内部讨论,消费者更爱哪个产品的市场调研,以及个人纠结的旅游地点选哪个,工作单位选哪个,恋爱对象选哪个。它是"选择困难症的福音",也是"顾此失彼的最优解"。
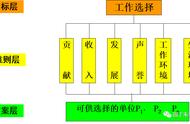
它有五个步骤构成,分别为建立层次结构,构建判断矩阵,指标权重计算、逻辑偏差校准、最优方案计算。

·层次结构分为目标层、因素层、方案层。
→目标层代表要解决的问题,例如找对象。
→因素层是解决问题时需要考虑的因素,例如对方的健康、相貌、经济、背景、价值观、习性等等。
→因素层可以是一级指标、二级指标,甚至是更多层级的指标构成。当由多层级构成时,相邻的两层中高层为目标层,低层为因素层,即在原有的层次关系中诞生出新一轮的层次关系。
→方案层是解决问题的各类方案,例如谈恋爱的三位候选人,富婆、姐姐、妹妹。
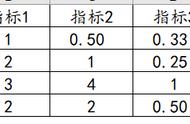
·层次构建完成后,即可构建判断矩阵。判断矩阵是将因素层的因素通过矩阵排列进行年龄比较,比较后的结果用标度表的数值表示。常见的标度表为1-9,分别对应同等重要、稍微重要、较强重要、强烈重要、极端重要,以及倒数和相邻判断的中间值。在比较的过程中矩阵的对角线均为自身与自身的比较,即横向的健康与纵向的健康相比属于同等重要,所以填写1即可。

其次在两两比较中它们之间的值互为倒数,即横向的健康与纵向的相貌相比健康若为5,那么横向的相貌与纵向的健康相比自然就是1/5,所以只需要判断对角线上面的数据即可。对角线下面的数据可以直接填写上面的倒数。
当判断矩阵填写完成后就可以开始计算每项因素的权重值。计算的过程中会涉及到一些数学的名词与计算公式,对这些不太了解的伙伴不用为难自己,只需要在excel里面按照视频的计算公式填写即可,这不影响对此方法的使用。计算公式一般为和积法或者方根法。
以方根法举例:
·第一步计算矩阵中的行积和,也就是按行相乘得到的因素数值。

·第二步将所得的行积和开n次方得到每行的特征向量,n代表每行因数的数量,若因数的数量为6就开60方。
·第三步将所得的特征向量归一化得出每项权重。规划指的是每行的特征向量除以特征向量的总和。现在得到的选中其实就属于每个指标对应的选中,但在举证的判断过程中往往会犯一些逻辑错误,例如a大于b大于c又大于a,所以还需要通过一次性检验来纠正逻辑错误。
检验的过程分三步:
·第一步构建a、w矩阵,a就是上述的判断矩阵,w就是规划后的特征向量。将判断矩阵的行乘以特征向量的列即可得出aw矩阵值,也就是b1乘借一加上b2乘借二加上b3乘借三加上等等。当然在excel里面可以通过函数来快速获得结果。