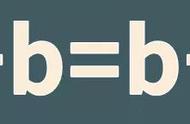人教版四年级下册,集中教学加法和乘法的五个运算定律。可是仔细看教材,是不是觉得加法交换律似乎没什么讲的,40 56=56 40,然后再举例子,归纳出加法交换律成立,学生也很好理解,似乎好像不用讲学生也明白,但仔细思考,书中只罗列了现象,至于为什么可以交换却没从本源上说清道理。只是用结果相同掩盖了过程的差别。就是用举例法归纳运用了心里已经知道的事儿。仔细想想,加法交换律为什么可以交换,能够交换的理由是什么?教材并没有从本源上说清道理,按照教材指示,归纳得出结论就好,甚至公开课都不能选加法交换律,因为实在“没有什么可以呈现”。

然而,根据课标“过程与方法的教学目标”凡是能够懂得道理,还是应该让学生经历过程并说清道理,仅仅用不完全归纳法就把加法交换律强加给学生似乎并不合情合理。
那么加法交换律的本源道理是什么呢?教学中如何让学生体验两个加数交换位置和不变的数学直观呢?
自然数的加法,其本源意义在于对两个具有有限基数且不相交的集合A和B作并集AUB之后,AUB的基数是A的基数与B的基数之和。
这样的解释小学生肯定不理解,但是说白了其实很简单。就是“数数”。A、B两堆石子,先数A堆的a颗,接着数B堆的b颗,最后的结果就是a b颗。加法的本质就是“接着数”。加法的概念不是来自于更多的小石子,而是来自于添加或合并的操作活动,如果从“数数”的本源学习加法交换律,是不是更直观呢?
不妨用朝三暮四的成语故事引入。

学生一定笑话猴子幼稚,其实是一样的,怎么证明是一样的?引导学生说出3个后面接着数4个是7个;4个后面接着数3个也是7个,能画点子图证明吗?

师:看来3 4还就等于4 3,加数变大还可以吗?请看例1……
你还能举几个例子吗?……
“数数”的过程看似简单,恰恰从数学的本质上解释了加法交换律,这样简单的数形结合,直观显示了3 4和4 3过程的差别,学生经历这样数学化的过程,不但知其然,更知其所以然,有利于从本质理解加法交换律。
运算律是运算的主要性质,反映了运算的规律性。学习运算律不仅仅是为了计算简便,更为重要的是发展学生对于数与运算意义的理解,培养数学学习的能力。加法交换律看似简单,却不能忽视数学本质,忽略数学基本活动。