我们准备来谈谈回归分析(回归分析?)的本质以及它的历史轶事,但无论如何,一窥回归分析的堂奥之前,还是有些观念需要先建立起来。
为何这么麻烦?把方法完整巡游一遍后,回头探讨基本结构是很有好处的,像是出国旅行,人生地不熟的时候,常常只能跟着人潮与旅行团规划走,但熟练的旅行者,会钻进街巷之中,寻找连结着城市各处的最短途径以及稍纵即逝的美丽风景。
首先,故事从这里开始:回归是什么?
时空来到好久好久以前,英国的达尔文(对,就是那个达尔文)有个谣传智商高达200的天才表弟叫Galton , Galton是个惊人的另类科学家,虽不是正统的学院学者,却出版了数以百计的书籍与论文,领域之广几乎无所不包,被尊称为「 Victorian Polymath 」。
Galton 身为伟大的达尔文的表弟,不意外地,他对遗传学也很有心得,并首创了优生学( Eugenics )用词。由于出身银行业兼军火商的家族, Galton 幸运地得以任意从事他喜爱的探险与科学活动,在1880 中期到1890 年代这段时间, Galton 找来了一群人做了各种人体特征的纪录,他得到两个心得:
第一,有两随机变数X 、 Y ,当其中一者的改变多少受到另一方的影响时,必然存在同时作用于此二者的因素,将这种关系定义为「有相关」,反之则为独立。
第二,当时人类遗传学开始相信优势是可以遗传给后代的,但是会不会持续下去则是未证实的疑问,譬如身高都很高的夫妻,是否会生下更高的儿女?

eugenic-statistics
Galton 发现,父母特征的确会遗传给后代,但是并不会产生极端身高的族群。当父母的身高已经远离平均身高时,生下的儿女身高并没有持续「远离」平均,而会稍微「靠近」平均,也就是相对矮了一点;反之父母身高很矮的后代,身高会相对其父母「靠近」平均一点。
当然双亲身高都很高的后代,比起双亲身高都很矮的后代,还是相对较高的,不过差距并未一直增加,反而会持续减少。
Galton把这个「极端」往「平均」移动的现象称为「 regression to the mean 」。用东方人的说法,就是「物极必反」,至于「极物」将「反向」何方?
Galton 说,这个答案就叫「平均数」。
Galton的第一项发现「相关系数r」,后来由另一位在统计史上名气鼎盛的Karl Pearson推导出线性通则,该式又名「Pearson积差相关系数」。
晚年的Galton与Pearson及Weldon关系相当好,不仅是研究伙伴,也资助二人创办了至今影响力仍巨的生物统计期刊《 Biometrika 》,在Galton的支持下,早期的《 Biometrika 》皆以超水准的规格发行,让该刊知名度大开, Galton过世以后也是由Pearson亲自为其整理传记。
Pearson的介绍,可参阅《卡方检定ON THE CROSS:PEARSON, YATES AND FISHER 》。
回归分析概念的可视化Galton 的回归概念,被逐渐补充、扩大,变得越来越完整,现在回归已是一个意义广泛的用词,更好的说法是「回归模型」,在这个模型底下包含了许多用以解释、判断、修正的诸多内容,若要产生一个「真正正确而有用」的模型所需的知识量,只看入门教科书绝对是不够的。
从模型整合的角度出发,所有回归都具有三个基本要件:
1. 系统成分( Systematic Component )
2. 随机成分( Random Component )
3. 连结函数( Link Function )
系统成分是给定的回归中,用来解释研究现象的元素,随机成分则是研究希望讨论的「未知」的现象。而「连结」就是描述系统成分与随机成分两者之间关系的函数。
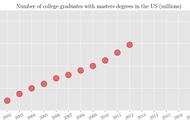
从文字定义似乎不易理解「回归」是什么,由图入手或许清楚得多,以下利用某地区房屋「坪数X 」对应「房价(单位:千万) Y 」的简回归( Simple Regression )范例说明之:

图中的圆点,是抽样的资料点,贯穿其中的直线,则是「回归直线」,回归直线的意义即是Galton 所谓的「平均」。残差e31 、 e33 分别表示第31 、 33 个资料点与平均线的差异,其余以此类推。其中,「坪数X 」就是系统成分,而「房价Y 」则是随机成分,对一个简单直线回归,连结函数就是线性方程式。
由于「回归到平均」的性质,观察回归直线与资料点的距离,即可推估该资料的一些特性,掌握这些数学特性,可以帮助我们做几件事:
1.可推估某资料点是否为「离群的极端值」。
2.可计算自变数X 与应变数Y 的相关性。
3.根据上述的相关性,可描述资料集的发展趋势。
4.拓展到拥有多个预测变数X 的「复回归」,可分析多个自变数与应变数的互动。
5.可大胆预测「资料集之外(括号外的部分)」的资讯,对应变数的可能影响。
例图用的是「线性回归」,然而回归用以描述自变数与应变数关系的函数不只有直线而已,二次或三次以上曲线、指数、对数、分段都是可行的方式,这也衍生出各种回归问题。
回归分析的公式化与残差以最普遍的直线回归为例,典型的线性回归式如下:

statistics-simple-linear-regression-example-2
此式称为「母体回归直线」,是描述「真实未知情况」的完美配适。但是因为完整、正确的普查在多数情况下几乎是不可行的,因此没人知道「真实情况」究竟是如何,退而求其次,统计学容忍些许错误的可能性,改以抽样资料推算真实的大概样貌。
样本回归直线因此诞生: