回归分析的基本原理,回归分析的原理和方法

statistics-simple-linear-regression-example-3

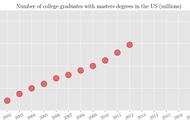
回归式中的「残差( Residual )」描述「观察资料Yi 」与「配适结果Yi-hat 」的差异，残差越小，代表模型的配适越接近观察资料，假如可证明观察资料之于真实情况具有代表性，就可利用配适结果对真实情况的良好描述进行有用的统计推论。

可以想像，对一个良好模型，其模型残差的期望值E( ei )应该要等于0。

残差的实际用法，改天再讨论，本文仅着重于残差与模型的关系描述。

在一般的直线回归中，残差的假设为：

image

有趣的是，其中残差的常态假设并非必要，虽然假设残差服从常态分配对很多人而言可能是理所当然的…，一些作者直接就把它写成基本假设，虽没有大问题却没交代清楚，其实还是有一点细微差别的。

先来看看为何残差不必要是常态分配？

根据高斯-马可夫定理( Gauss-Markov Theorem )，以「最小平方法( Least Squares Method )」计算线性回归参数b0 、 bi将有「最佳线性不偏估计量( BLUE ， Best Linear Unbiased Estimator )」性质的前提，要求残差符合以下条件：

1. 残差期望值为0 。

2. 残差具有同质变异，变异数为一固定常数。

3.残差间没有自相关( Autocorrelation )。

4.自变数与残差无关，即「正交性( Orthogonality )」。

发现了吗？最小平方法下的残差其实是不需要常态假设的。关于回归系数的最小平方估计，可参阅《一场关于猜的魔术：统计估计的形成》。

regression-introduction

回到回归分析的主题上，针对残差假设为常态分配的意义有三：

第一，回归是需要相对大样本才较有意义的方法，特别是多元变数的复回归，对样本的需求量很大，很自然会符合中央极限定理。实务上，笔者会建议300-500 个样本或是更多时才适用。

第二，统计推论常见的Z 、 T 、 Chi-squared 、F基本上都是跟常态的机率分布性质( Normal Distribution )有关，光是有残差，要是无法对残差进行推论也是不够力的。

第三，系数检定用的T 分配及类T 统计量都是对偏离常态不太敏感的统计量，因为它们本身就是常态Z 统计量的近似，因此近似又近似的结果就是，除非是残差真实分配远离常态，不然影响非常有限。在稍大的样本条件下更是如此(理由同第一点)。

那有没有残差不为常态的回归模型范例？

有的，像Logistic回归式就没有残差的假设，因为「根本没有残差」，那是因为推导中代换掉的关系，有机会再来谈。

回到残差的分配对模型的影响上，记得常态分配具有「水平位移」的特性吗？

对模型：

statistics-regression-residual-normal-distribution

由此可知，当假定残差服从常态分配时，其实也就等于假定Y将服从常态分配，期望值E( Y )= b0 biX … bkX ，变异数与残差相同。

应该有人看过教科书这么说：对Y 而言，假设其为常态分配…，理由可以从这里找到。

在回归里，残差变异数的估计量数是MSE ( Mean Squared Error )，因此回归线的变异数也等于MSE ，记得以前做专题还看过一个很烂的翻译叫做「均方差」…，天啊，什么东西？

假如你也被书中一下子说残差变异数、一下子说模型变异数、一下子均方差搞得糊里糊涂，那么现在应该松一口气了，因为都是同一件事。

所以一般说的直线回归究竟是不是常态的方法？

某个程度上视你从什么角度切入。基本上，回归的分配取决于残差的假设，而XY对应关系则决定回归的函数形式。在上述的直线模型中，假如只有一个自变项，通常称为简回归或简单直线回归( Simple Regression )，同时存在多个自变项的情形，称为复回归或多元回归( Multiple Regression )，两者在许多基本性质上可以直接推广，不过在复回归，容易产生因多元变数而起的模型问题，是以在统计教学中通常会将两者分开讨论。

简回归的式子其实就是国中学过的Y = a*X b ，但在统计上描述得更实务、更精细，直线回归基本特性，可由符号下标看出来：

第一，每一组样本Xi1~Xik 对应到一个应变数Yi (函数基本定义)。

第二，截距项与斜率项在回归配适完成之后就固定住了，因此可以任意代入想观察的自变数组合，或者稍作修正，做资料集外的「预测」，做讨论比较时也很方便…，总之这种一目了然的形式深受分析人员喜爱。

接着来谈谈回归函数的形式吧。

如果从自变数「 X 」与应变数「 Y 」的函数反应形状来决定回归的「线性」，那么我们基本上可以得到三个种类：直线、曲线与非线。

但是！对于这几种对应关系的回归称呼，似乎没有一致的标准。

举个例子来说好了，某些作者会用「线性」来表示「直线 曲线」，但问题是曲线在没有充分指定的情况下是非常任意的，也就是所有的对应关系都是广义的曲线，其实直线本身也不过曲率= 0的曲线特例罢了。

另一些作者，用「线性」代表「直线」，非线性代表「广义的曲线」，这个分法本身就有误导之嫌，毕竟线性不等于直线，在书目之前来来去去很容易混为一谈。

至于直线与非直线的区别，曾看过这样的分法：直线回归永远是「一阶式」，只要是「二阶」以上式子基本上就是非直线。但是这个有点可议…，等一下的例子告诉你为什么。