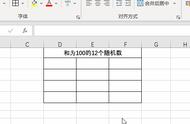
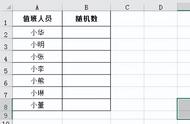
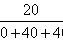伪随机 PRNG 生成的序列并不是真随机。它完全是由一个初始值决定,初始值称为随机种子(seed)。接近于真随机序列可以通过硬件随机数生成器生成。但是伪随机数生成器因为其生成速度和可再现的优势,实践中也很重要。
寻找一个合适的随机算法是非常重要的。
一个实验的每一个 variant (实验组或对照组)都具有关于 users 的一个随机抽样。随机算法必须有一些特征。特征如下:
- 特征(1):用户必须等可能看到一个实验的每个 variant,对于任意的 variant 必须是无偏的。
- 特征(2):同一个实验中,对于单个 user 重复分配必须是一致的,对于该用户每次后续访问中,该 user 必须被分配到相同的 variant 上。
- 特征(3):当多个实验同时并行运行的时候,实验之间必须没有关联关系。也就是在一个实验中,一个 user 被分配到一个 variant,对于被分配给其他任意实验的一个 variant,在概率上没有影响。
- 特征(4):算法必须支持单调递增的,也就是说,如果没有对那些已经被分配给实验组的用户分配进行变更,用户看到一个实验组的百分比可能会缓慢增加的。
3.3.1 使用 caching 的伪随机
伪随机数的随机性可以用它的统计特性来衡量,主要特征是每个数出现的可能性和它出现时与数序中其他数的关系。
伪随机数的优点是它的计算比较简单,而且只使用少数的数值很难推断出它的计算算法。
使用 caching 缓存,可以使用标准伪数字生成器作为随机算法,一个好的伪数字生成器会满足特征(1)和特征(3)。
对于特征(2),需要引入状态,用户的分配必须被缓存,或者缓存完成可以是数据库存储,便于下次再次访问应用。
3.3.2 hash 和分区
不同于伪随机方法,hash 和分区是无状态的,每一个 user 都会被分配一个唯一的 user_unique_id,使用 ssid 和 webid (或者其他)来维持。user_unique_id 会和实验的 id 进行映射绑定,接着 user_unique_id 和实验 id 使用 hash 函数来获得一个整数,整数的范围是均匀分布的。
hash 函数的选取需要注意⚠️,如果 hash 函数有漏斗(那些相邻 key 的实例会映射到相同的 hash code),会造成均匀分布的冲突,如果 hash 函数有特性(某一个 key 变动会产生一个 hash code 上可预测的变动),会造成实验之间会发生相关。
「加密 hash 函数 MD5 」生成的数据在实验间没有相关性。其实还可以关注「大质数素数 hash 算法」等更加精密优良的算法。
3.4 实验灰度发布
实验发布是一个容易忽略但又非常重要的步骤,从比较小的流量慢慢发布到相对比较大的流量,直到最后全站发布。这个过程是需要自动化和风险控制相结合。
我们经常的做法就是:
- 实验发布之后,还可以预留一些流量来衡量实验的长期效果。
- 还可以重复发布某一个实验,看实验的结果是否可以保持。
选取什么指标来进行检测,从而更好的帮助我们进行数据驱动决策。
对于一个应用或者产品来说,可能会有很多指标的选择,哪些指标需要被重点关注,哪些仅仅是关注,哪些是可以不关注。为什么要定义这个指标,这个指标的定义是为了说明什么情况,如果这个指标发生变化,将需要怎么去解释它。
4.1 指标特性
选取什么指标来进行检测,从而更好的帮助我们进行数据驱动决策。

对于一个应用或者产品来说,可能会有很多指标的选择,哪些指标需要被重点关注,哪些仅仅是关注,哪些是可以不关注。为什么要定义这个指标,这个指标的定义是为了说明什么情况,如果这个指标发生变化,将需要怎么去解释它。
4.1.1 按照实验的角度来划分
核心指标:需要优化的目标指标,决定这个实验的最终发展方向。这种指标在一个实验是非常少的,在运行之后是不做改变的。
非核心指标指标:与核心指标有因果关系的 基础数据的指标,基础数据的指标是应用运行的底线。
4.1.2 指标敏感性和鲁棒性
指标敏感性:指标对所关心的事物是否足够敏感。
指标鲁棒性:指标对不关心的事物是否足够不敏感。
可以通过预先小规模试验来验证,或者 AA 试验来排除伪关系。
4.1.3 指标分类
(1)计数或者求和(比如:访问页面的用户数)。
(2)指标分布的平均数,中位数,百分位。
(3)概率与比率。
(4)比例。
4.2 自顶向下设计指标
(1)高层次的指标(比如:活跃用户数,点击转化率 CTR 等等)。
(2)指标细节(比如:如何定义用户活跃)。
(3)使用一组指标,并将它们整合成一个单一指标(比如:总体评价指标 OEC )。
总体评价指标 OEC :如果是使用一套指标,可以把他们聚合成一个指标,比如构造一个目标函数,或者是简单的加权指标。比如 OEC = A * 0.6 B * 04 C * 2 。
现在我们的策略是指标,还是独立去观测。那为啥不使用 OEC 来看指标呢?通过 OEC 看的指标不能单独观测多个指标,对于新手小白比较友好,只需要关注 OEC,不需要关注多个指标的数据,但是并不能真的反应多个指标的真实情况。
举个例子:
点击率的定义:
- 定义一:登陆后总点击次数 / 登陆后的去重后的访问总数
- 定义二:被点击的页面数 / 总页面数
- 定义三:总的页面点击次数 / 总页面数

有了 AB 实验,并且有实验指标选取之后,实验结果的分析就成为一件非常重要而且有挑战的事情。
产生一组数据很容易,但是从数据中分析得到实验的洞察(Insight)并不简单。
5.1 实验结果显著
上面有说到实验结果的可信度,接下来详细来介绍。
说到实验结果是否显著,我们需要知道统计学中 2 类统计错误,我们简单说明一下,这里我们不展开说。
5.1.1 两类统计学错误
在统计学的世界里,我们往往只说概率,不说确定,在现实世界中往往只能基于样本进行推断。在 AB 实验中,我们 不知道真实情况是什么,因此做假设检验的时候就会犯错误,这种错误可以划分为两类:
- 这是第一类错误:实际没有区别,但实验结果表示有区别,我们得到显著结果因此否定原假设,认为实验组更优,发生的概率用 表示。
- 这是第二类错误:实际有区别,但是实际结果表示没有区别,我们得到不显著的结果因此无法拒绝原假设,认为实验组和对照组没有区别,发生的概率用 表示。
理想状态下当然是希望可以同时控制这两类错误,但是这是不可能的,两个概率值之间是负向关系,其中一个值的减少必然伴随着另一个值的增大,为什么呢?后续有机会再分享。
5.1.2 显著和可信的判断
是否显著,是否可信,我们可以通过以下几种因素来判断:
(1)p 值。展示该指标在实验中犯第一类错误的概率,该概率小于显著性水平 α ,统计学中称为显著, 1-α 为置信度或置信水平。
- 简单来说:p 值判断不同版本的实验结果之间不存在显著差异的概率。
- p-value 越小越可信,有显著差异的指标,P-value=0.01 的比 P-value=0.05 的可信度更高。
- p 值基本上还有另一个相对应的叫作 t 值,这个 p 值其实就是在 t 分布下 ≥t 值的概率密度值 (P(x≥t))。

通常情况下:
p 值 > α(显著水平α,α 值一般 5%) ,说明 A 版本和 B 版本没有太大差别,不存在显著性差异。
p 值 < α(显著水平,α 值一般 5%),说明 A 版本和 B 版本有很大的差别,存在显著性差异。
我们根据判断 p 值和第一类错误概率 α 比较,已经做了决策。是不是觉得大功告成,不,我们可以继续考虑 power 统计功效来衡量实验的可信。也就是我们要同时考虑第二类错误概率,这时候引入 power 统计功效。
(2)power 统计功效(1 - )。实验能正确做出存在差异判断的概率。
- 可以理解为有多少的把握认为版本之间有差别。
- 该值越大则表示概率越大、功效越充分。
- 一般来说,我们一般并设置的最低的统计功效值为 80% 以上。认为这样的可信度是可以接受的。
举个例子:
实验 A 显示,power(统计功效)为 92%,那么就可以理解为有 92% 的把握认为版本 A 和版本 B 之间是有差别的。
但是 power 根本算不出来,power 作为需要满足的前提条件,作为先验的输入值。
- 实验开启前,通过流量计算器中计算流量和实验运行时长。
- 实验开启后,通过 power=80%,然后计算 MDE。
(3)MDE 检验灵敏度,能有效检验出指标置信度的 diff 幅度。
通过比较指标 MDE 与指标的目标提升率来 判断不显著的结论是否 solid,可以避免实验在灵敏度不足的情况下被过早作出非显著结论而结束,错失有潜力的 feature。
MDE 越小,说明当前的实验灵敏度越高, 并且可以认为:实验组相比于对照组,只有高于 MDE 的提升才能大概率检测出效果显著。小于 MDE 的提升,大概率不会被检测出显著。
- 当前条件:指当前样本量,指标值和指标分布情况,并假设样本方差与总体指标方差足够接近。
- 有效检测:指检出概率大于等于 80%(也就是犯第二类错误概率 <=20%)
- 主要影响因素:样本量大小
举个例子
假设你对该指标的预期目标提升率为 1%。
- 如果此时 MDE = 0.5%,MDE < 预期提升值,说明指标变化真的不显著,请结合业务 ROI 和其他维度里例如用户体验、长期战略价值等来综合判断是否值得上线。
- 如果那此时 MDE = 2%,MDE > 预期提升值,说明当前能检验出显著性的最小差异值是 2%,由于灵敏度不足未能检测出。这种情况下建议增大样本量, 例如扩大流量、再观察一段时间积累更多进组用户,指标还有置信的可能。
(4)置信区间。置信区间就是用来对一个概率样本的总体参数的进行区间估计的样本均值范围。一般来说,我们使用 95% 的置信水平来进行区间估计。
置信区间可以辅助确定版本间是否有存在显著差异的可能性:
- 如果置信区间上下限的值同为正或负,认为存在有显著差异的可能性。
- 如果同时正负值,那么则认为不存在有显著差异的可能性。
在火山引擎 AB 测试的实验报告中,指标分析的详细视图中有个值叫相对差,该值就是指标变化的点估计值,而置信区间给出的是指标预期变化的区间估计值,区间估计值有更大的可能性覆盖到指标相对变化的真实值。(假设做 100 次实验,有 95 次算出的置信区间包含了真实值)。
可以这样简单但不严谨地解读置信区间 :假设策略全量上线,你有 95% 的把握会看到真实的指标收益在 置信区间 这个范围内。
5.1.3 决策流程