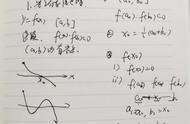今天这道题目呢,涉及到数学当中的一个概念,就是二分法求多项式单根。
二分法求函数根的原理为:如果连续函数f(x)在区间[a,b]的两个端点取值异号,也就是f(a)f(b)<0,则它在这个区间内至少存在1个根r,即f(r)=0。
这道题目把二分法求函数根的原理告诉了我们,但仅仅依靠这个来做这道题目,是做不出来的,还是得看题目的具体要求。
具体要求这道题目的具体要求,就是讲清楚了二分法的步骤:
1、检查区间长度,如果小于给定阈值,则停止,输出区间中点(a b)/2;否则
2、如果f(a)f(b)<0,则计算中点的值也就是f((a b)/2)。
3、如果中点的值f((a b)/2)恰好是0,那么,这个区间中点(a b)/2正好是所要求的根,否则
4、如果中点的值与f(a)同号,就说明根在区间[(a b)/2,b]之间,令a=(a b)/2,重复循环
5、同理,如果中点的值与f(b)同号,就说明根在区间[a,(a b)/2]之间,令b=(a b)/2,重复循环
这道题目呢,是要求计算给定的三阶多项式的根。
也就是f(x)=a3x^3 a2x^2 a1x a0这个三阶多项式的根。

理清楚逻辑是这道题目最大的难点,也是最为关键的地方。
1、首先,我们来看二分法的第一个步骤,检查区间长度,如果小于给定阈值,则停止。
这里的给定阈值指的是什么呢,我不知道,我也不清楚,这个阈值是题目中没有给出来的条件,所以需要自己去网上查找相关的资料。
大家都知道,二分法的目的是将区间的两个端点都靠近零点的值,也就是说两个端点之间的距离越接近0越好,那么什么值最接近0呢。
我们以本道题目为例,输出样例要保留两位小数,那么以两位小数的最小值为阈值是否可以呢。
区间长度毫无疑问就是b-a,那么给定阈值正如我们推测的一样,用0.01来代替。
我们可以先这么假设,之后再进行修改也完全来得及。
也就是说,第一个条件语句需要用到的,就是对b-a是小于还是大于0.01来进行一个判断。
如果大于等于0.01的话,才会继续往下走。
2、之后根据“如果”这个关键词,来梳理出所有的条件语句。
对f(a)*f(b)进行一个判断,再对中点的值f((a b)/2)进行一个判断。
3、在对中点的值f((a b)/2)进行一个判断的基础上,再对该值是否等于0进行一个判断,满足为0的要求后,再对与f(a)和f(b)是否同号进行一个判断,分别得到最终的结果。

//二分法求多项式单根
#include<stdio.h>
#include<math.h>
int main(){
float a3=0;//第一个系数
float a2=0;//第二个系数
float a1=0;//第三个系数
float a0=0;//第四个系数
float m;//(a b)/2
float a;//区间a
float b;//区间b
float x;//结果
scanf("%f %f %f %f",&a3,&a2,&a1,&a0);
scanf("%f %f",&a,&b);//按照给定格式输入
float f(float q){//函数
return a3*pow(q,3) a2*pow(q,2) a1*q a0;
}
while((b-a)>=0.01){//我这边用到的阈值是0.01
m = (a b)/2;
if(f(m)==0){//如果中点的值为0,停止用break
x = (a b)/2;
break;
}
if(f(a)==0){//对区间端点a要进行一个单独判断
x = a;
break;
}
if(f(b)==0){//对区间端点b要进行一个单独判断
x=b;
break;
}
if(f(m)*f(a)>=0){//f((a b)/2)与f(a)同号时
a = m;
}
if(f(m)*f(b)>=0){//f((a b)/2)与f(b)同号时
b = m;
}
}
if((b-a)<0.01){//小于阈值时,直接打印
x = (a b)/2;
}
printf("%.2f", x);
}结果测试


注意,这道题目主要有四个测试点,虽然只有一个循环,但是这道题目是很容易出现运行超时的问题的,运行超时可不仅仅与循环有关,还与调用函数次数、数值大小n也有关系,都是需要注意的地方。
总结这道题目着实存在一些难度,在完成这道题目的时候,我也遇到了不少问题。
我在这篇文章中给出的代码结果是正确的,但是我在写代码的时候,产生了不少错误。
比方说:
1、我把m=(a b)/2放在了循环外,那样的话,m就是一个固定的值,不会发生变化,而循环内的m,应该是一个动态的(a b)/2,所以就产生了数值不匹配的问题。
2、算幂次方用到一个pow函数,pow(x,3)表示x的三次方,这是需要注意的。
3、在发现出现运行超时问题的时候,不妨可以使用函数来代替。
比方说重新定义一个函数float f(float x),然后在该函数内返回对应的方程式,达到一个能够用于调用的状态。
正如这道题目一样:
float f(float q){//函数
return a3*pow(q,3) a2*pow(q,2) a1*q a0;
}
这就需要我们静下心来,安安静静地读清楚读明白这道题目,然后梳理好逻辑,一步一步去解决遇到的问题,这样的话,我们才能很好地提升自己的编程能力。